Дараалуулан тавьсан 8 сандалд дөрвөн хүү, дөрвөн охиныг суулгах болжээ. Ингэхдээ тэгш дугаартай суудалд эрэгтэйг харин сондгой дугаартай суудалд охиныг суулгана. Үүнийг хичнээн аргаар хийж болох вэ?
Бодолт
Бодолтыг ойлгохын тулд эхлээд Комбинаторикийн томьёог ойлгох хичээлийг үзэхийг зөвлөе.
Эхний хүү дөрвөн сандлын алинд ч суух боломжтой, хоёрдахь хүү үлдсэн гурваас харин гуравдахь нь үлдсэн хоёрын аль нэгэнд сууж болно. Дөрөвдэх хүүд ганц л боломж үлдэнэ. Үржих дүрмийн дагуу дөрвөн суудалд хүү нар 4·3·2·1=24 янзаар суух боломжтой. Өөрөөр хэлбэл энэ нь 4 -өөс үүсгэх сэлгэмэл буюу 4!=1·2·3·4=24 гэсэн үг. Сайн ойлгохгүй байвал 1,2,3,4 цифрүүдээр 4 оронтой 1234, 1243, 1324, 1342 гэх мэтээр тоог зохиогоод тоолоод үзээрэй.
Охид ч гэсэн бас ийм боломжуудтай тул үржих дүрмийн дагуу охид, хөвгүүд суудлуудад 24·24=576 янзаар суух боломжтой.
Хариу
576





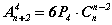 тэгшитгэл бод.
тэгшитгэл бод.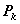 - k - элементээс зохиосон сэлгэмэл бол
- k - элементээс зохиосон сэлгэмэл бол 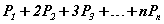 илэрхийллийг хялбарчил
илэрхийллийг хялбарчил задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.