16 см суурьтай, 10 см хажуу талтай адил хажуут гурвалжин өгөгджээ. Гурвалжинд багтсан болон гурвалжинг багтаасан тойргуудын радиус болон тойргуудын төв хоорондын зайны нийлбэрийг ол.
Бодолт
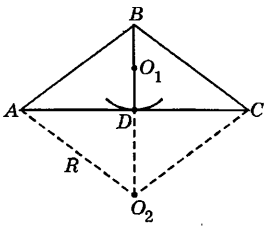Бодлогын нөхцлөөр зургийг тоймлон гаргая. O1 , O2 бол гурвалжинд багтсан болон багтаасан тойргуудын төв. Гурвалжинг багтаасан тойргийн радиусийг 
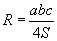харин багтсан тойргийн радиусийг 
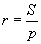томьёонуудаар олдог.
Нөхцөлд гурвалжингийн талуудыг өгсөн бас аль ч томьёонд гурвалжны талбай орж байгаа тул ABC гурвалжны талбайг Героний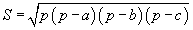 
томьёогоор тооцвол 
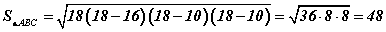гэж гарна. Томьёоны p=(16+10+10)/2=18 периметрийн хагас гэдгийг сануулъя. Багтаасан тойргийн радиусийг R харин багтсан тойргийн радиусийг r гээд томьёонуудыг ашиглан тооцвол 
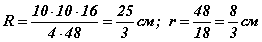гэж гарна. Зургаас тойргуудын төв хоорондын зай 
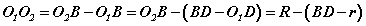гэдэг нь тодорхой. Гурвалжин адил хажуут тул BD нь түүний өндөр бөгөөд Пифагорийн теоремоор 
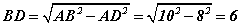гэдгээс тойргуудын төв хоорондын зай 
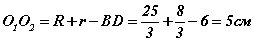гэж гарна. Эндээс олох ёстой хэмжээсүүдийн нийлбэр 
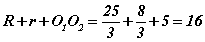байна.
Хариу
16
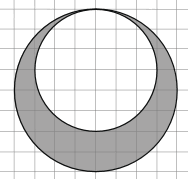Дөрвөлжин шугамтай цаасан дээр хоёр тойргийг зуржээ. Дотор талын тойргийн талбай 9 бол будагдсан хэсгийн талбайг ол.
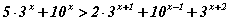тэнцэтгэл бишийг бод.
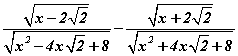илэрхийллийн x=3 утгыг ол.