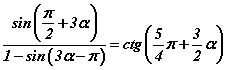адитгалыг батал.
Бодолт
Өгөгдсөн илэрхийллийг хувиргалтын томьёогоор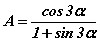 
хэлбэрт оруулъя. Хувиргалтын буюу гаргалтын томьёонууд хичээлийг үз. Одоо гурвалсан өнцгийн задаргааны томьёог хэрэглээд явж болох ч адитгалын нөгөө талд 3α/2 өнцөг байгааг харгалзан үзээд 3α өнцгийг 
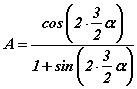гэж задлаад давхар өнцгийн 
, 
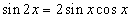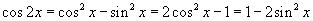томьёонуудаар задалбал 
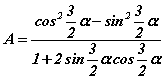болно. Цааш 
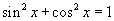болон 
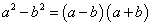томьёонуудыг ашиглан хувиргавал 
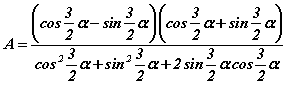хэлбэрт шилжинэ. Хуваарт нийлбэрийн квадратийн 
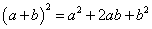томьёо байгаа тул 
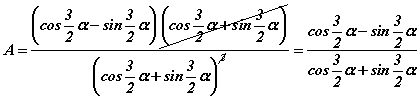болно. Бутархайн хүртвэр, хуваарийг 
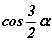-д хуваавал 
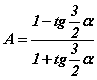болно. Адитгалын баруун хэсгийг гаргахын тулд tgπ/4=1 адитгалыг ашиглан цааш хувиргавал 
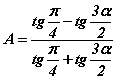болно. Хуваарт 
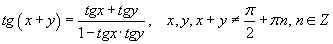томьёог ашиглавал 
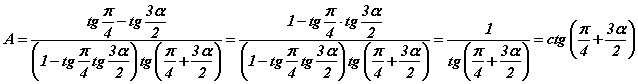гээд котангенс функц гарч ирнэ. Цааш котангенс функцийн чанарыг ашиглавал 
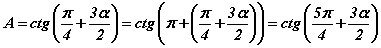болсноор адитгал батлагдана.
Зөвлөмж: Ийм бодлого нилээд түвшин өндөртэй шалгалт, шүүлэгт ирэх магадлалтай. Бодлогын онцлог гэвэл маш олон тооны чанар, томьёонуудыг ашиглаж байгаагийн дээр тригнометрийн илэрхийллийг өөрийн хүссэн хэлбэрт хувиргаж болохыг харуулсанд оршино. Илэрхийллийн хувиргалт бол бодлого бодох суурь гэдгийг сануулъя.
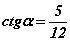ба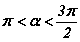 
бол sinα=?
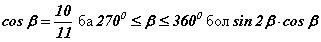тоон утгыг ол.
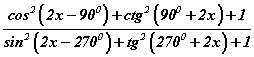илэрхийллийг хялбарчил.
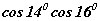илэрхийллийг нийлбэрт шилжүүлбэл 
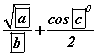болох бол a, b, c -г ол
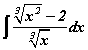интеграл бод
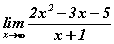хязгаарыг бод.
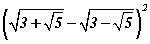утгыг ол.