|x-2|=|x-3|+2 тэгшитгэл хэдэн шийдтэй вэ?
Бодолт
Модултай бодлого сурагчдад нилээд хүндрэл дагуулдаг. Ухагдхууныг нэг мөр сайн ойлговол асуудал тийм ч хүнд биш гэдгийг Модултай тэгшитгэлийг бодох хичээлийг үзэн ойлгон аваарай.
Өгөгдсөн тэгшитгэлийн тодорхойлогдох муж ]-∞; +∞[ байна. Өөрөөр хэлбэл тэгшитгэл бүх тоон шулуунд тодорхойлогдоно гэсэн үг.
Модултай тэгшитгэлийг бодох универсал аргачлалын дагуу тэгшитгэл дэх модул бүрийг тэгтэй тэнцүүлэхэд үүсэх тэгшитгэлийг бодвол x-2=0 -> x=2; x-3=0 -> x=3; гэж гарна. Гарсан шийдүүд тэгшитгэлийн тодорхойлогдох мужийг ]-∞; 2[, [2; 3[, [3; +∞[ гэсэн гурван интервалд хуваана. Одоо интервал тус бүрээр анхдагч тэгшитгэлийг бодъё.
- ]-∞; 2[ завсарт тэгшитгэлийн модул дахь функцууд бүгд сөрөг утгатай тул модулаас -(x-2)=-(x-3)+2 гэж чөлөөлөгдөнө. Тэгшитгэлээс 0=3 гэсэн буруу тэнцэл үүсэх тул ]-∞; 2[ завсарт тэгшитгэл шийдгүй.
- [2; 3[ завсарт |x-2| модул эерэг харин |x-3| модул сөрөг утгатай тул модулаас x-2=-(x-3)+2 гэж чөлөөлөгдөнө. Тэгшитгэлийн x-2=-x+3+2 -> 2x=7 -> x=3,5 шийд [2; 3[ завсарт харьяалагдахгүй тул анхдагч тэгшитгэлийн шийд болж чадахгүй.
- [3; +∞[ завсарт тэгшитгэлийн модул дахь функцууд бүгд эерэг утгатай тул модулаас x-2=x-3+2 гэж чөлөөлөгдөнө. Тэгшитгэлээс 0=1 гэсэн буруу тэнцэл үүсэх тул ]3; +∞[ завсарт тэгшитгэл шийдгүй.
Тэгшитгэлийн шийд ]-∞; 2[, [2; 3[, [3; +∞[ интервалуудаас олдсон шийдүүдийн нэгдэл байх ёстой. Дээрх тооцоогоор тэгшитгэл аль ч интервалд шийдгүй тул анхдагч тэгшитгэл шийдгүй.
Тэгшитгэлийн модул доторх функцууд шугаман тул бодлогыг графикийн аргаар хөнгөн шийдэх боломжтой. Тэнцүүгийн тэмдгийн хоёр тал дахь функцуудийн графикийг байгуулбал
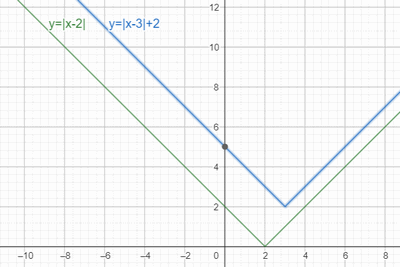
байна. Эндээс графикуудад огтлолцол байхгүй тул тэгшитгэл шийдгүй нь шууд харагдана. Графикийг байгуулахад модул ухагдхууныг сайн ойлгосон байх шаардлагатай нь ойлгомжтой. Модулаас дандаа эерэг тоо гарна гэдгийг мэддэг бол модулууд тэг авах x -ийн утгаас хоёр тийш 2 утга олоход л графикийг төвөггүй байгуулна.
Зөвлөмж: Энгийн шугаман тэгшитгэлийн хувьд графикийн арга хурдан боловч ерөнхий тохиолдолд модултай тэгшитгэлийг бодох универсал аргачлал илүү.
Хариу
шийдгүй
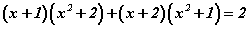тэгшитгэлийг бод.
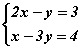системийг бод
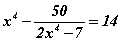тэгшитгэлийг бод.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.