x+y+z=7 тэгшитгэл хэдэн натурал шийдтэй вэ?
Бодолт
Натурал шийдийн тоог олох тул x≠0; y≠0; z≠0; байх ёстой. Тэг натурал тоонд ордоггүйг сануулъя. Бодлогын нөхцөлд x; y; z; хувьсагчдын авах утганд натурал тоо гэснээс өөр хязгаарлалт байхгүй байгаа нь тоонууд тэнцүү утгуудтай байж болно гэсэн үг. 3 натурал тооны нийлбэр 7 байх бүх боломжийг олно гэсэн үг. Тэгшитгэл алгебрийн тэгшитгэл хэлбэрийнх боловч m элементээс n -ээр зохиосон дараалал хамаарахгүй давталттай хэсэглэлийн тоог олох комбинаторикийн бодлого юм.
Тэгшитгэлийг m ижил бөмбөлөгийг n хайрцагт (m≥n) хайрцагууд хоосон байхгүйгээр хичнээн аргаар байршуулж болох вэ? гэж үзэж болно. Манай тохиолдолд x; y; z; хувьсагчдыг хайрцаг харин бөмбөлөгийн тоог 7 гэж үзье. Тэгшитгэлийн натурал шийдүүдийн тоог олох нөхцлөөр хайрцагууд хоосон байж болохгүй /хувьсагчид 0 утгатай авахгүй./ тул эхлээд хайрцаг бүрд нэг нэг бөмбөлөг хийгээд үлдсэн 7-3 бөмбөлөгийг хайрцагуудад дурын байдлаар хувиарлан хийвэл тэдгээрийн нийлбэр 7 той тэнцэнэ. Боломжийн тоог m элементээс n -ээр зохиосон дараалал хамаарахгүй давталттай хэсэглэлийн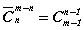 
томьёогоор тооцдог. Томьёоны дагуу боломжийн тоо буюу тэгшитгэлийн натурал шийдийн тоо 
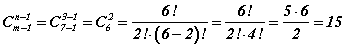гэж гарна.
Бодолтын аргачлалыг сайн ойлгон авахыг зөвлөе.
Бодлогыг stars and bars гэж нэрлэдэг аргачлалаар хөнгөн олох боломжтой ч энэ аргачлалыг ЕБС-д үздэггүй болов уу. Холбоосоор орон теоремийг харвал тэгшитгэлийн хувьд n=7, k=3 гэдгээс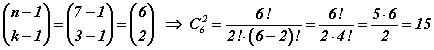 
гэж гарна.
Шалгалт дээр бодлогыг бодоход хүндрэл үүсвэл x+y+z=7 тэгшитгэлийн натурал шийдүүдийг хугацаа илүү зарцуулах сонгох аргаар шийдэх гэж үзсэн ч болох юм. Жишээ нь 1 + 1 + 5 = 7; 1 + 2 + 4 =7; 1 + 3 + 3 = 7; 2 + 1 + 4 = 7; ... гэх мэтээр.
Зөвлөмж: Шалгалтад ирсэн бүх тоог шийдэх албагүй тул хүндрэл үүссэн эсхүл бодох аргачлалыг олохгүй байгаа даалгаваруудыг шууд орхиод цаг үлдвэл оролдох нь дээр гэдгийг зөвлөе.
Хариу
15
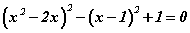тэгшитгэлийг бод.
тэгшитгэлийг бод.
тэгшитгэлий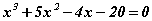н язгуурууд x1 , x2 , x3 бол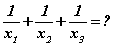 
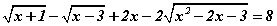тэгшитгэлийг бодъё. Тэгшитгэлийн тодорхойлогдох муж нь x≥3. Энэ мужид 
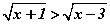тул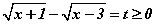 
гэж орлуулбал анхны тэгшитгэл 
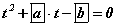тэгшитгэлд шилжинэ. Эндээс 
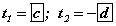гэж гарах ба 
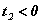учир нөхцөлд тохирохгүй. Орлуулгаа буцааж бодвол тэгшитгэлийн шийд 
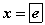гэж гарна.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.