a, b тэг биш хоёр векторын хувьд |a+b| = |a-b| бол эдгээр векторууд перпендикуляр гэдгийг батал.
Бодолт
|a+b| = |a-b| гэдгээс |a+b|2 = |a-b|2 байна.
|a+b|2=(a+b)(a+b)=|a|2+2a·b+|b|2 ба |a-b|2=(a-b)(a-b)=|a|2-2a·b+|b|2 байдаг тул |a+b|2=|a-b|2 тэнцлээс a·b=0 гэдэг нь гарч ирнэ. Тэг биш хоёр векторын скаляр үржвэр нь зөвхөн эдгээр векторууд перпендикуляр байхад л тэгтэй тэнцүү байна.
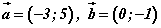векторууд өгөгдсөн бол 
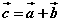векторийн координатийг ол.
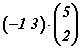матрицуудын үржвэрийг олоорой.
тэгшитгэлийг бод.
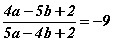бол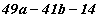 
илэрхийллийн утгыг ол.