Дэлгүүрт бие биеэсээ үл хамаарах хоёр автомат машин ажиллах ба тэдгээрийн аль нэг нь ажиллахгүй болох магадлал 0,05 бол дор хаяад нэг машин ажиллаж байх магадлалыг ол.
Бодолт
Бид дор хаяад нэг автомат ажиллаж байх магадлалыг олох хэрэгтэй. Автоматуудын хувьд ажиллаж байх магадлал 0,95 харин ажиллахгүй байх магадлал 0,05 байна. Хоёр автоматын хувьд + ажиллаж байх, - ажиллахгүй байх гэж үзвэл бидэнд (+, +); (+, -); (-, +); (-, -) гэсэн 4 тохиолдол гарч ирнэ. Эдгээрээс бодлогын нөхцөлд (+, +); (+, -); (-, +); гурав тохирно. Эдгээр үзэгдлүүдийн магадлалуудыг олоод нэмбэл бодлогын хариу гарах ёстой. Автоматууд бие биеэсээ хамааралгүй ажиллах тул (+, +) үзэгдлийн магадлал P(1)=0,95·0,95=0,9025; (+, -); (-, +); үзэгдлийн магадлал тэнцүү буюу P(2)=0,95·0,05=0,0475; P(3)=0,05·0,95=0,0475; байна. (+, +); (+, -); (-, +); гурван үзэгдэл нийцэхгүй үзэгдлүүд өөрөөр хэлбэл зэрэг тохиохгүй гэхдээ аль нэг нь тохиож байвал бодлогын нөхцөлд тохирох тул магадлалын нийлбэр нь бодлогын хариу болно. Эндээс P=P(1)+P(2)+P(3)=0,9025+0,0475+0,0475=0,9975 болно.
Бодлогыг энгийн аргаар бодохыг үзүүлье. (+, +); (+, -); (-, +); (-, -) гэсэн 4 тохиолдолын нэг нь л бодлогын нөхцөлд тохирохгүй. Тэгэхлээр тэр үзэгдлийн магадлалыг олоод 1 -ээс хасвал нөгөө гуравын магадлал гарч ирнэ. Автоматууд хоёулаа ажиллахгүй байх магадлал бол тэдгээрийн ажиллахгүй байх магадлалын үржвэр байна. Яагаад гэдгийг өөрсдөө олоорой. Ингээд P=1-P(4)=1-0,05·0,05=1-0,0025=0,9975 гарна.
Магадлалын бодлогыг бодох хичээлийг үз.
Хариу
0,9975





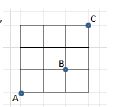 A цэгээс эхлэн эсвэл дээш 1 нэгж, эсвэл баруун тийш 1 нэгж явсаар B цэгийг дайран C цэгт очих бүх ялгаатай замыг ол.
A цэгээс эхлэн эсвэл дээш 1 нэгж, эсвэл баруун тийш 1 нэгж явсаар B цэгийг дайран C цэгт очих бүх ялгаатай замыг ол. илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.