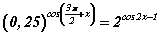 тэгшитгэл
тэгшитгэл 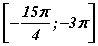 завсарт хэдэн шийдтэй вэ?
завсарт хэдэн шийдтэй вэ?
Бодолт
Илтгэгч тэгшитгэлд тригнометрийн функц орж ирсэн. Ийм бодлого сурагчдыг айлгаж магадгүй. Энд илтгэгч функцын чанарыг мэдэж байхад энгийн хувиргалт хийгээд тригнометрийн тэгшитгэлд шилжүүлээд бодолтыг хийнэ. Эхлээд 0,25 -ыг 2 -ын -2 зэрэг гэдгийг олоод харах хэрэгтэй. Үнэхээр 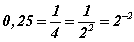 байгаа биз дээ. Тэгвэл өгөгдсөн тэгшитгэлийг
байгаа биз дээ. Тэгвэл өгөгдсөн тэгшитгэлийг 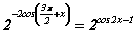 гэж үзэж болно. Ижил сууриудын зэргүүд тэнцүү байхад л тэд тэнцэх ёстой тул
гэж үзэж болно. Ижил сууриудын зэргүүд тэнцүү байхад л тэд тэнцэх ёстой тул 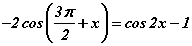 байна. Косинус давхар өнцгийн
байна. Косинус давхар өнцгийн 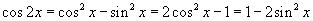 , нийлбэрийн
, нийлбэрийн 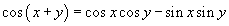 томьёонуудыг ашиглан хувиргалт хийвэл
томьёонуудыг ашиглан хувиргалт хийвэл
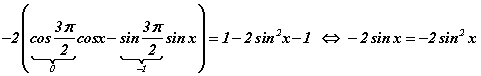 болно. Хэрвээ гаргалтын томьёог мэддэг бол шууд түүнийг ашиглаж болно. Гэхдээ нийлбэр, ялгаварын томьёо бол тригнометрийн бусад томьсонуудыг гаргах үндсэн хэрэгсэл болдог тул эдгээрийг цээжээр мэдэж байх нь тустай. Тэгшитгэлийг цааш бодвол
болно. Хэрвээ гаргалтын томьёог мэддэг бол шууд түүнийг ашиглаж болно. Гэхдээ нийлбэр, ялгаварын томьёо бол тригнометрийн бусад томьсонуудыг гаргах үндсэн хэрэгсэл болдог тул эдгээрийг цээжээр мэдэж байх нь тустай. Тэгшитгэлийг цааш бодвол 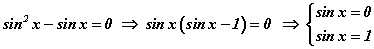 болно. Шийдийг нэгж тойргийг ашиглан олцгооё.
болно. Шийдийг нэгж тойргийг ашиглан олцгооё.
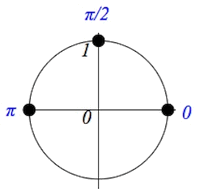 Үүний тулд нэгж тойрог дээрээ синус 0, 1 утга авах цэгүүдийг тэмдэглэнэ. Синус π/2 дээр 1 харин 0 ээс π гээр үелэн тэг утга авдаг функц. Энгийн тэгшитгэлийн шийдийг цээжээр мэддэг байх нь цаг алдахгүй хурдан бодох суурь болно. Эндээс тэгшитгэлийн шийдүүд
Үүний тулд нэгж тойрог дээрээ синус 0, 1 утга авах цэгүүдийг тэмдэглэнэ. Синус π/2 дээр 1 харин 0 ээс π гээр үелэн тэг утга авдаг функц. Энгийн тэгшитгэлийн шийдийг цээжээр мэддэг байх нь цаг алдахгүй хурдан бодох суурь болно. Эндээс тэгшитгэлийн шийдүүд
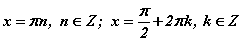 гэж гарна.
гэж гарна.
Сурагчид шийдийг олж чаддаг мөртлөө ерөнхий шийдийн бичилтийг ойлгохгүй байх нь элбэг байдаг. Тригнометрийн функцууд үелэх чанартай. Эндээс л шийд дээр үеийг оруулан өгөх шаардлага гардаг. Өөрөөр хэлбэл тригнометрийн функцууд тодорхой үеэр нэг утгыг хязгааргүй олон давтан авдаг. Иймээс шийдийг олонлог хэлбэрээр гаргадаг. Зурагт үзүүлсэн тойрог 2π үеэр давтагдаад байх учраас үе бүр дээр шийдүүд давтагдана гэдгийг
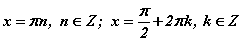 гэж бичээд байгаа юм.
гэж бичээд байгаа юм.
Зургаас харвал sinx=0 нь тойрог дээр 0, π дээр тэг утгыг авч байгаа. Нэг тойрог дээр 2 удаа тэг утга авах тул шийдийн олонлог π давтамжаар харин sinx=1 нь тойрог дээр нэг удаа л 1 утга авах учраас 2π давтамжийг авч байгаа юм. Илүү дэлгэрэнгүйг сайтын Тригнометрийн бодолтын жишээ хичээлээс үзээрэй. Онолыг сайн ойлгохгүйгээр бодлогыг зөв бодох эсхүл бодолтыг ойлгох хэцүү. Бодлого бүрийн бодолтод онолын тайлбар оруулаад байх нь боломжгүй.
 Тэгшитгэлийн шийдийг олсон тул дараагийн хэсэг болох
Тэгшитгэлийн шийдийг олсон тул дараагийн хэсэг болох 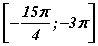 завсар дахь шийдүүдийг олох ажилдаа орцгооё. Шийдийг сонгох бодлогод үелэх чанарыг ойлгохгүй бол сонголт хийх бараг боломжгүй. Иймээс шийдийн талаар илүү дэлгэрэнгүй тайлбарласан болно.
завсар дахь шийдүүдийг олох ажилдаа орцгооё. Шийдийг сонгох бодлогод үелэх чанарыг ойлгохгүй бол сонголт хийх бараг боломжгүй. Иймээс шийдийн талаар илүү дэлгэрэнгүй тайлбарласан болно.
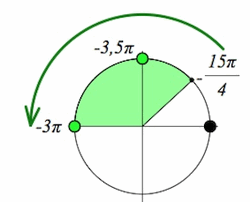
Шийдийн сонголтыг хийхдээ нэгж тойргийг хэрхэн ашиглахыг авч үзье. Зураг өмнөхтэй ижилхэн бас нэгэн тойрог. Гэхдээ энд тойрог тэнхлэгийн сөрөг чиглэлд өөрөөр хэлбэл n=-3, k=-2 байх үед харагдах байдал. Тойргийн энэ хэсэгт манай завсар орж байгаа. Түүнийг зурагт ногоон өнгөөр тэмдэглэсэн. Шийдүүд n=-3, k=-2 байх үед завсарт орох учраас хариунд π гийн давтамжийн коэффициентүүдэд өөр утгуудыг тавиад байгаа хэрэг. Завсар тодорхой болсон болохоор эндээс тэгшитгэлийг хангах утгууд өмнөх зурагт үзүүлсэн байрлалд одоо өөр өнцгийн хэмжээстэй харагдана. Энд бол бодит утгууд бий болно. Завсар өгөгдсөн тул бидэнд шийдийн π гийн давтамж хэрэггүй болсон. Утгуудыг олохын тулд π гийн давтамжийг ашигласан. Ингээд тэгшитгэл 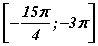 завсар -3π, -3,5π гэсэн шийдүүдтэй. Эндээс бодлогын хариу 2 гэдэг нь ойлгомжтой.
завсар -3π, -3,5π гэсэн шийдүүдтэй. Эндээс бодлогын хариу 2 гэдэг нь ойлгомжтой.
Жич: Бодолтыг сайн ойлгохыг хичээгээрэй. Материал таалагдсан бол найз нөхөддөө share хийн манай сайтыг дэмжихийг хүсье.
Хариу
2





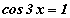 тэгшитгэл бод.
тэгшитгэл бод.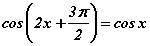 тэгшитгэлийг бод.
тэгшитгэлийг бод.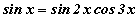 тэгшитгэлийг бод.
тэгшитгэлийг бод.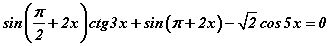 тэгшитгэлийг бод.
тэгшитгэлийг бод.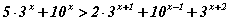 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.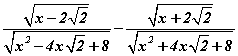 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.