Энэ нийтлэлээр бодит шалгалт дээр ирж байсан тригнометрийн хоёр бодлогын бодолтыг дэлгэрэнгүйгээр тайлбарлах болно. Эдгээр бодлогын бодолтыг сайн судлаад ойлговол тригнометрийн бодлогыг ойлгоход сайн суурь болж чадна. Бодлогын шийдүүдээс өгөгдсөн завсар дахь утгуудыг сонгох нэмэлт нөхцөл оруулсан нь сурагчдаас тригнометрийн илүү нарийн ойлголтыг шаардах юм. Сурагчид бодлогыг хураангуйлан энгийн хэлбэрт оруулж чаддаг ч шийдийг гаргах тэр тусмаа өгөгдсөн завсарт харьяалагдах шийдийг сонгохдоо үндсэн хүндрэлтэй тулдаг. Иймд бодолтуудыг анхааралтай судлаад ойлгон авахыг хичээгээрэй. Олон бодлого бодохдоо биш аргачлалыг ойлгох нь чухал.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
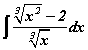интеграл бод
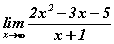хязгаарыг бод.
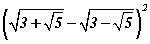утгыг ол.