Арифметикийн үйлдлүүд нэг ба хоёрдугаар түвшингийн гэж хуваагдана.
- Нэмэх ба хасах үйлдлүүд бол нэгдүгээр түвшингийнх. Жишээ нь 5+4 - нэмэх, 7-3 хасах
- Үржих ба хуваах үйлдлүүд бол хоёрдугаар түвшингийнх. Жишээ нь 5·4 - үржих, 12:3 хуваах
Үйлдлийн дараалал
Илэрхийлэл хаалт агуулаагүй зөвхөн нэг түвшингийн үйлдлүүдийг агуулж байвал үйлдлүүд зүүнээс баруун тийш тэдгээрийн дарааллын дагуу хийгдэнэ.
Жишээ 1
15+17-20+8-12 илэрхийллийн утгыг ол.
Бодолт
Өгөгдсөн илэрхийлэлд хаалт байхгүй зөвхөн 1-р түвшингийн (нэмэх, хасах) үйлдлүүд байгаа тул үйлдлийн дарааллыг тогтоовол дээрх дүрмийн дагуу
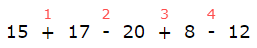
байна. Дарааллын дагуу үйлдлүүдийг хийвэл
- 15+17=32
- 32-20=12
- 12+8=20
- 20-12=8
гээд илэрхийллийн утга 15+17-20+8-12=8 гэж гарна.
Жишээ 2
60:15·7:2·3 илэрхийллийн утгыг ол.
Бодолт
Өгөгдсөн илэрхийлэлд хаалт байхгүй зөвхөн 2-р түвшингийн (үржих, хуваах) үйлдлүүд байгаа тул дүрмийн дагуу үйлдлийн дарааллыг тогтоовол
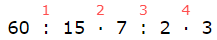
байна. Дарааллын дагуу үйлдлүүдийг хийвэл
- 60:15=4
- 4·7=28
- 28:2=14
- 14·3=42
гээд илэрхийллийн утга 60:15·7:2·3=42 гэж гарна.
Илэрхийлэл хаалт агуулаагүй хоёр түвшингийн үйлдлүүдийг агуулж байвал эхлээд хоёрдугаар түвшингийн үйлдлүүдийг зүүнээс баруун тийш тэдгээрийн дарааллын дагуу хийгээд дараа нь нэгдүгээр түвшингийн үйлдлүүдийг мөн ижил дарааллаар гүйцэтгэнэ.
Жишээ
24 : 3 + 5 · 2 - 17 илэрхийллийн утгыг ол.
Бодолт
Өгөгдсөн илэрхийлэл 1-р түвшингийн 2, 2-р түвшингийн 2 үйлдлүүдийг агуулж байгаа. Үйлдлүүд дарааллыг дүрмийн дагуу тогтоовол эхний үйлдэл хуваах, хоёрдахь нь - үржих, гуравдахь нь - нэмэх, дөрөвдэх нь - хасах үйлдэл буюу
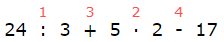
байна. Дарааллын дагуу үйлдлүүдийг гүйцэтгэвэл
- 24 : 3 = 8
- 5 · 2 = 10
- 8 + 10 = 18
- 18 - 17 = 1
гээд илэрхийллийн утга 24 : 3 + 5 · 2 - 17 = 1 гэж гарна.
Зөвлөмж: Арифметикийг эхлэн үзэж буй сурагчид дадлага хийн үйлдлийн дарааллын энэ дүрмийг сайн тогтоон авбал сайн суурь болохыг сануулъя. Үйлдлийн дарааллын дүрмийг яваандаа сурдаг гэж анхааралгүй хандах нь цаашид нилээд асуудал үүсгэх магадлалтайг санаарай.
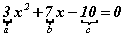a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.