Алгебр (арифметикийн адилаар) тоотой холбоотой төрөл бүрийн асуудлын шийдийг олох шинжлэх ухаан. Арифметик, алгебрын хоорондоо нилээд ялгаатай. Алгебр тоотой биш тоог төлөөлөх үсгүүдтэй голлон ажилладаг бол арифметикт тодорхой тоонууд дээр тухайн асуудлын шийдлийг олоход чиглэдэг. Эндээс эдгээр хоёр салбар ухааны гол ялгаа гэвэл алгебр асуудлын ерөнхий шийдлийг харин арифметик асуудлын тухайн тохиолдлын шийдлийг судалдагт оршино.
Алгебр арифметикийн ялгааг илүү ойлгомжтой тайлбарлахын тулд дараах бодлогыг аваад үзье.
Хоёр аялагч бие биеэ угталцан хоорондоо 240 км зайтай хоёр хотоос нэгэн зэрэг гарчээ. Эхнийх нь өдөрт 25 км харин хоёрдахь нь 35 км явдаг бол тэд хэд хоногийн дараа уулзах вэ?
Арифметик аргаар дээрх бодлогыг бодъё.
- Аялагчдын өдөрт туулах замыг өгсөн болохоор тэд өдөрт нийлээд 25+35=60 км замыг туулна.
- Тэгвэл тэднийг тусгаарлаж буй 240 км замыг тэд 240:60=4 хоногт туулан уулзана гээд шийдийг олно.
Тэгвэл дээрх бодлогыг 240, 25, 35 гэсэн гурван тооны хувьд биш илүү ерөнхий байдлаар шийдэх гээд үзье. Өөрөөр хэлбэл бодлогын өгүүлбэр дэх 240, 25, 35 тоонуудыг a, b, c үсгээр сольё. Өөрөөр хэлбэл a - хоёр хотын хоорондын зай харин b - эхний аялагчийн c - хоёрдахь аялагчийн өдөрт туулах зай гэсэн үг.
Ийм ерөнхий тохиолдолд алгебрийн аргачлал орж ирэх ч бодолтын алгоритм өөрчлөгдөхгүй.
- Аялагчдын өдөрт туулах нийт зам b+c байна.
- Аялагчид өдөрт нийлээд b+c зайг туулдаг бол тэд нийт a зайг
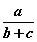 гээд бодлогын шийдийг олно.
гээд бодлогын шийдийг олно.
Сүүлийн 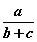 шийд бол дээрх төрлийн бодлогын ерөнхий шийд юм. Одоо энэ шийдэд a=240, b=25, c=35 тоонуудыг тавивал 4 гэж л гарна.
шийд бол дээрх төрлийн бодлогын ерөнхий шийд юм. Одоо энэ шийдэд a=240, b=25, c=35 тоонуудыг тавивал 4 гэж л гарна.
Үсгэн буюу ерөнхий шийдэл тоон шийдэл буюу тухайн тохиолдлын шийдлээс
- Ерөнхий шийдэл дээрхтэй төстэй нэг төрлийн бүх бодлогод тохирно. Жишээ нь 240, 25, 35 тоонуудын оронд 360, 20, 40 тоонууд өгөгдсөн бол тоонуудыг ерөнхий шийдэд тавиад тооцоход
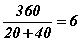 гэж гарна.
гэж гарна. - Үсгэн илэрхийллээр асуудлын шийдийг олоход өгөгдсөн тоонууд дээр ямар үйлдлийг ямар дарааллаар хийх нь маш тодорхой харагдана.
- Дээрхтэй төстэй асуудлын шийдэлд тухайн биетийн нэр эсхүл ойлголт, бодлогын өгөгдлүүд зэрэг нь тийм ч гол утгыг илэрхийлэхгүй байгааг анзаарвал бодлогыг ерөнхий хэлбэрт шилжүүлэх боломжийг нээдэг зэргээр давуу талуудтай.
Иймээс дээрх бодлогыг дараах байдлаар
Жишээ нь
хоёр биет хоорондоо a нэгж зайтай (нэгжээр метр, километр, өртөө гэх мэтээр) хоёр газраас нэг зэрэг бие биеэ угталцан гарчээ. Эхний биет нэгж хугацаанд (хоног, цаг, минут г.м) b, хоёрдахь биет c нэгж зайг туулна. Тэгвэл тэд хичнээн нэгж хугацааны дараа уулзах вэ? гэж
нэгдсэн хэлбэрт шилжүүлж болно.
Бодлогын шийдэл бол 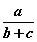 байх нь ойлгомжтой. Энэ бичлэгийг ерөнхий томьёо гэж нэрлэдэг. Томьёо бидэнд дээрхтэй ижил нөхцөлтэй дурын бодлогыг ямар нэгэн үндэслэл гаргалгүйгээр шууд нэг тооцооллоор шийдэх боломжийг олгоно.
байх нь ойлгомжтой. Энэ бичлэгийг ерөнхий томьёо гэж нэрлэдэг. Томьёо бидэнд дээрхтэй ижил нөхцөлтэй дурын бодлогыг ямар нэгэн үндэслэл гаргалгүйгээр шууд нэг тооцооллоор шийдэх боломжийг олгоно.
Эндээс алгебр тоотой хамааралтай асуудлын ерөнхий шийдийг олон эдгээр асуудлуудыг нэгтгэх зорилготой. Үүний зэрэгцээ алгебр эдгээр ерөнхий шийдлийг хамгийн энгийн ойлгомжтой хэлбэрт оруулах асуудлыг судлахын зэрэгцээ нэг үсгэн илэрхийллийг түүнтэй адил өөр үсгэн хэлбэрт оруулахад сургадаг.
Арифметикаас алгебрт шилжих үед сурагчид нилээд сандардаг. Тоонуудын оронд үсэг орж ирсэн болохоос алгебр бол арифметикийн үргэлжлэл асуудал болон түүний шийдлийг ерөнхийлөлд оруулах л салбар ухаан тул бүр ч илүү сонирхолтой гоё хичээл.
Алгебр тийм хүнд биш гэдгийг дараагийн хичээлүүдээс ойлгон математикт дуртай болно гэдэгт итгэж байна.





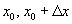 цэгүүд дээрх
цэгүүд дээрх 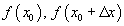 утгуудыг авч үзье.
утгуудыг авч үзье. 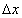 -г
-г 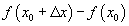
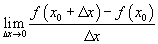 хязгаарыг x0 цэг дээрх f(x) функцын
хязгаарыг x0 цэг дээрх f(x) функцын 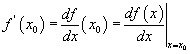 гэж тэмдэглэдэг.
гэж тэмдэглэдэг. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.