Тоог хэдэн нэгжээр, хэд дахин эсхүл тодорхой хувиар багасгаж болно.
Нэгжээр багасгах.
Тоог нэг эсхүл хэдэн нэгжээр багасгана гэдэг нь тухайн тооноос багасгах хэрэгтэй нэгжийг хасна гэсэн үг. Жишээ нь 13 -ыг 2 -оор багасгана гэдэг нь байгаа 13 нэгжээс 2 нэгжийг хасахийг хэлнэ.Үр дүнд нь 11 гарна. Эндээс "арвангуравыг хоёроор багасгах", "аравангураваас хоёрыг хасах" зэрэг нь эхний тооноос дараагийн тоог хасахийг л илэрхийлнэ.
Жишээ
15 -аас 4 ийг хас.
13 -ыг 2 -оор багасга
Бодолт
15 - 4 = 11
13 - 2 = 11
Нэрлэсэн тооны хувьд тухайн тоог багасгахдаа тоологдож буй зүйлтэй тохирох нэгжийг хасах ёстой.
Жишээ
Дүүд 10 алим, 8 жүрж байжээ. Тэр ахдаа 3 алим, 2 жүрж эгчдээ 1 алим, 3 жүрж өгсөн бол дүү хэдэн алим, хэдэн жүржтэй үлдэх вэ?
Бодолт
Дүүд хоёр төрлийн жимс байсан бөгөөд тэр ах, эгчдээ өгсөн жимсүүд нэрлэсэн тоогоор өгөгдсөн тул нэрлэсэн тоог багасгах дүрмээр 10 - 3 - 1 = 6 алим, 8 - 2 - 3 = 3 жүржтэй үлдэнэ. Хэрвээ дүү хэдэн жимстэй үлдсэн бэ гэж асуусан бол алим, жүрж хоёр хоёулаа жимс тул 18 - 3 - 2 - 1 - 3 = 9 жимстэй үлдэнэ гэсэн хариу гарна.
Санамж: Тоог багасгахдаа нэрлэсэн эсхүл тодорхойгүй тоогоор багасгах эсэхийг зөв ойлгох хэрэгтэй.
Хэд дахин багасгах
Тоог хэд дахин багасгана гэдэг нь тухайн тоог хуваагдагч болгоод хэд дахин гэсэн удаа хуваах хэрэгтэй.
Жишээ нь 15 -ыг 3 дахин хасагдуул гэвэл 15 -ыг хуваагдагчаар аваад гуравт хуваана. Өөрөөр хэлбэл 15 : 3 = 5 гэсэн үг. Үр дүнд нь 5 гарна.
Жишээ
Хайрцагт 10 харандаа түүнээс 2 дахин бага үзэг байжээ. Тэгвэл хайрцагт хэдэн үзэг байсан бэ?
Бодолт
Үзэг харандаанаас 2 дахин бага гэсэн тул 10 -ыг хуваагдагч болгоод 2 -т хуваана гэсэн үг. Ингээд 10 : 2 = 5 (үзэг) гэж гарна.
Жишээ
Хашааны баруун хэсэг 9 модтой харин зүүн хэсэгт баруун хэсгээс 3 дахин бага модтой бол хашаа хэдэн модтой вэ?
Бодолт
Эхлээд хашааны зүүн хэсэгт ургаж буй моднуудыг тоог олохын тулд баруун хэсгийн модны тоог 3 дахин багсагах ёстой бөгөөд 9 : 3 = 3 (мод) гэж гарна. Дараа нь хашаан доторх нийт модны тоо бол хоёр хэсгийн моднуудын нийлбэр буюу 9 + 3 = 12 (мод) байна.
Хувиар нэмэгдүүлэх
Тоог тодорхой хувиар багасгах гэдэг нь тухайн тоог багасгах хувьтай тэнцэх хэсгийг тодорхойлоод түүнийг өгөгдсөнтэй тооноос хасах үйлдэл юм.
Жишээ
300 -г 10 хувиар багасга гэсэн бол эхлээд 300 -гийн 10% (300:100)·10=30 гэдгийг олоод цааш 30 -ийг 300 гаас хасан 300 - 30 = 270 -ийг гэдгийг олох юм.
Тоог хувиар багасгах үйлдлүүдийг нэг үйлдлээр хураангуйлахыг дараах жишээгээр харцгаая.
Жишээ
80 -ыг 20 хувиар багасга. Тооцоог 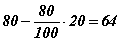 гэж нэг үйлдлээр гүйцэтгэж болно. Энд өмнөх жишээний аргачлал болон хувиар багасгах дүрмийг нэг үйлдлээр л хийсэн байгаа.
гэж нэг үйлдлээр гүйцэтгэж болно. Энд өмнөх жишээний аргачлал болон хувиар багасгах дүрмийг нэг үйлдлээр л хийсэн байгаа.
Бодлогын бодолтоос x тоог y хувиар багасгахыг 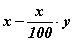 томьёогоор илэрхийлэх буюу тооцож болно гэдэг нь харагдана. Томьёог ашиглан ямарч тоог хэдэн ч хувиар багасгах боломжтой гэдгийг өөрсдөө туршин шалгаарай.
томьёогоор илэрхийлэх буюу тооцож болно гэдэг нь харагдана. Томьёог ашиглан ямарч тоог хэдэн ч хувиар багасгах боломжтой гэдгийг өөрсдөө туршин шалгаарай.





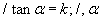 өнцөг үүсгэсэн шулуун байна. / Зур. 8 / Иймээс порпорционалын коэффициентыг бас
өнцөг үүсгэсэн шулуун байна. / Зур. 8 / Иймээс порпорционалын коэффициентыг бас 
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.