Хоёр морь дийлэхгүй ажил

Энд хүртэл үзсэн төгсгөлүүдэд хүчтэй тал нь эсрэг ноёнг мадлах хангалттай хүчтэй байсан. Хүчний давуутай тал нь ганц ноёнг мадлахын тулд хамгийн багадаа ямар давуу хүчтэй байх хэрэгтэй вэ?  Үзсэн төгсгөлүүд дундаас мад хийхэд хамгийн бага хүч оролцсон нь тэргээр мадлах байлаа. Тэгвэл хоёр морь энэ даалгаварыг биелүүлж чадах уу гэсэн асуулт гарч ирнэ. Үнэндээ бол харьцуулсан үнэлгээгээр хоёр морь нь нэг тэрэгнээс хүчтэй шүү дээ. Үүнээс гадна хоёр хөнгөн бод ганц ноёнг хангалттай мадлаж байсан.
Гэтэл сул тал зөв хамгаалж чадвал хоёр морь (өөрийн ноёны дэмжлэгтэйгээр ч гэсэн) эсрэг талаа мадалж дийлдэггүй.

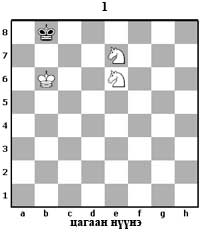
1 ба 2-р диаграмд хүчтэй тал нь эсрэг ноёноо буланд бараг шахаад байна. Шатруудын зөв харилцан ажиллагааны дүнд ноёнг буланд шахах нь тийм ч хэцүү биш. Одоо эсрэг ноёнг мадлахад гол хүчээ гаргах хэрэгтэй байдаг. Гэтэл харамсалтай нь хоёр моринд ийм боломж байдаггүй. Яагаад гэдгийг харцгаая.
1-р диаграмын байрлалаас цагаан 1. Мe7-c6+ гэвэл хар 1. ... Нa8?? гэж орж болохгүй. Учир нь 2. Мc7X гээд маданд орно. Иймд 1. ... Нb8-c8! гэж булангаас гарна. 2. Мc5 (эсвэл 2. Мf8) гэж хар ноёнг хоргоох гэвэл пад болно. Хэрвээ 2. Мe5 гэвэл 2. ... Нb8 ын дараа хар ноёны буцах замыг хаан түүнийг буланд хэрхэн оруулах нь харагдахгүй болно. Тэгвэл өөрөөр үзье.
1. Мc5 Нa8 2. Мe4 (2. Мd7, 2. Мa6, 2. Мc6 нүүдлүүд нь пад болгоно) 2. ... Нb8  3. Мd6 Нa8  4. Мd5 Нa8 дахиад юу ч болсонгүй. Дахиад нэг оролдоод үзье. 1. Мd4 Нa8  2. Мb5 Нb8  3. Мa7 Нa8  4. Мd5 Нb8  5. Мb4 Нa8 дахиад л ижил үр дүн. Хар ноёнд хаанаас нь ч хүрч болдоггүй.


Эсрэгээрээ 2-р диаграмд цагаан ноёнд булан аврал болно.
1. ... Мf4-h3+ 2. Нg1-h1 (эсвэл 2. Нg2 гээд чөлөөтэй болно. Харин 2. Нf1?? гэж орвол 2. ... Мe3X болох тул орж болохгүй.) Хэрхэн мадлах нь харагдахгүй байна.
1. ... Нd1-e1 2. Нg1-h1 Мg4-e3 3. Нh1-h2 Нe1-f2 4. Нh2-h1 хөөлт ямарч амжилтгүй дууслаа. 1 ба 2 -р диаграмд нүүдлийн ээлж нөгөө талдаа байсан ч юу ч өөрчлөгдөхгүй.

Иймээс энэ төгсгөлд хамгаалагч тал сүүлийн шатанд өөрөөр хэлбэл зах болон буланд анхааралтай байхад л маданд орохгүй. Зэрэгтэй шатарчид ийм байрлал үүсвэл тэнцээгээр тохиролцдог.

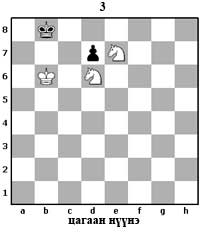Гэхдээ сул талд хүү байвал хүчний ийм харьцаа нь нөгөө талд ашигтай байдлыг бий болгодог. 3-р диаграмыг авч үзье.

Энд тоглолт дараах байдлаар үргэлжилж болно.
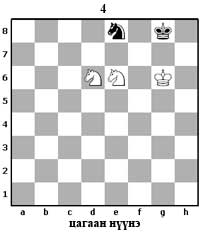1. Мd5 Нa8 2. Мc7+ Нb8 3. Мa6+! Нa8 4. Мb5! хар талд хүү байгаагүй байсан бол пад болно  4. d6 5. Мbc7X

4-р диаграмд хар морь өөрийн ноёнд туслахаар юм шиг харагдаж байна. Гэвч морь маш муу байрлалтай тул түүнээс ямар ч тусалцаа хараад хэрэггүй болсон.

1. Мf7! Мd6 хар тал өөрийн хэрэггүй морийг хаяж байна. Цагаан занганд орсонгүй. 2. Мh6+! Нh8 3. Мg5! хар цугцвангд орсон 3. ... Мf5 морины ямарч өөр нүүдэл тус болохгүй 4. Мgf7X
4. Н:f5? байсан бол тэнцээ болох байлаа.

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Хөлөлгөөний зарчмууд

  Нээгдсэн тоо: 1977 Төлбөртэй

Арон Исаевич Нимцовичийн "Миний систем" гэдэг шатрын номоос үргэлжлүүлэн таницуулъя.

Тав. Хурцадмал байдлыг даран хөлөлгөөний эсхүл тоглолтын чөлөөлөлтийг хийх. Тоглолтын чөлөөт хөлөлгөөнд саад болсон өрсөлдөгчийн эсрэг маневрууд асуудал үүсгэж эхэлбэл ийм байдлыг шийдвэртэй, хурдан дуусгах шаардлагатай. Энд хагас дутуу шийдэл байж таарахгүй. Үүнийг дараах жишээгээр тайлбарлая. 1. e4 e5 2. Мf3 Мc6 3. d4 d5. Харын сүүлийн нүүдэл эрсдэлтэй. Цагааны 3. d4 идэвхитэй нүүдэлд хар яг ийм байдлаар шууд хариу барих гэсний хэрэггүй. Энэ нь цаашдын зарим хүндрэлүүдийн эх үүсвэр. 4. exd5 Бxd5 5. Мc3 Тb4. Хар гараанд бэрсээрээ хоёрдахь нүүдэл хийх асуудлаас түр салсан. Гэвч 6. Тd2 -ийн дараа зарим нэгэн хүндрэл гарч ирсэн. Бэрсээ хөдөлгөх нь темп алдахад хүргэнэ.

Бэрсний хүүнүүдийн гараа

  Нээгдсэн тоо: 1162 Бүртгүүлэх

Гараа бэрсний гамбитийн c2-c4 нүүдэлтэй холбоогүй бэрсний хүүг түлхэн эхэлдэг хэсэг системийг нэгтгэсэн. Цагаан эхний нүүдлээс төвд хурцадмал байдал үүсгэлгүйгээр өрсөлдөгчид үргэлжлэлийн сонголтыг өгдөг нь тоглолтыг тэнцвэржүүлэх тэмцлийг хөнгөн болгодог.

[Event "Бэрсний хүүнүүдийн гараа. Левицкийн дайралт."] 1. d4 d5 2. Bg5 h6 (2... c5 3. dxc5 f6 4. Bh4 e5 5. e4 dxe4 6. Qxd8+ Kxd8 7. Nc3 Bxc5 8. O-O-O+ {гээд цагааны дарамттай. (Ходжсон - Ван Вели, 1995)}) 3. Bh4 c6 {цагааны хар хөлийн тэмээ бэрсний жигүүрээс холдсонг ашиглан хар бэрсээ b6 дээр гаргахаар бэлтгэсэн.} 4. Nf3 (4. e3 {гэвэл} Qb6 5. Qc1 e5 6. Nf3 e4 7. Nfd2 Ne7 8. c4 Nf5 {гээд хард асуудалгүй. (Миладинович - Дегерман, 1999)}) 4... Qb6 5. b3 Bf5 6. e3 e6 7. Bd3 Bxd3 8. Qxd3 Nd7 {хар өөрийн хүчийг амжилттай задалж чадсан.} 9. c4 Ne7! 10. c5 Qa5+ 11. Nc3 b6! {санаачлага харын талд. (Ананд - Карпов, 1998)}
Бэрсний хүүний гараа

  Нээгдсэн тоо: 618 Нийтийн

Хагас хаалттай гараа багц хичээлийн сүүлийн гараа болох Бэрсний хүүний гарааг танилцуулая. Шатарыг гайгуй суръя гэвэл гарааны онолыг нилээд суурьтай судлах хэрэгтэй. Иймд сайтын Багц хичээлүүд хэсгээс шатрын гарааны хичээлүүдийг сонирхохыг зөвлөе. Гарааны онолын мэдлэг муугаас үүдэн эхний нүүдлүүдэд алдаа хийн хожигдох явдал шатар сонирхогчдын дунд маш түгээмэл байдаг. 

[Event "Бэрсний хүүний гараа. 1-р хэсэг"] 1. d4 {энэ гараа цагаан өргийг 1. d2-d4 нүүдлээр эхлүүлээд c2-c4 түлхэлтэд яардаггүй хэдэн системийг нэгтэгдэг.} Nf6 2. Bg5 {харилцан боломжуудтай хурц тоглолтод хүргэдэг Тромповскийн дайралт гэж нэрлэдэг бага судлагдсан үргэлжлэл.} Ne4 ({цагаан бат бэх хүүний төв үүсгэх} 2... e6 {боломжтой ч хард хоёр тэмээний давууг өгдөг.} 3. e4 h6 4. Bxf6 Qxf6 5. Nc3 d6 (5... Bb4!?) 6. Qd2 g5 7. Bc4 Nc6 8. Nge2 Bg7 9. Rd1 Bd7 10. O-O O-O-O 11. Nb5 {тоглолтын санаачлага цагаанд. (Ананд - Карпов, 1998)}) (2... c5 3. Bxf6 gxf6 4. d5 Qb6 {үргэлжлэл нарийн тоглолтод хүргэнэ.}) 3. Bh4 (3. Bf4 c5 4. d5 Qb6 5. Bc1 e6 6. f3 Qa5+!? 7. c3 Nf6 8. e4 d6 {нарийн тоглолттой үргэлжлэл тохиолдож байсан. (Ван дер Виль - Каспаров, 1982)}) (3. h4!? {нүүдэл сонирхолтой. (Миладинович - Сулскис, 1994)}) 3... d5 (3... c5 {хариулт боломжтой. Жишээ нь} 4. f3 g5! 5. fxe4 gxh4 6. e3 Bh6 7. Kf2! (7. Qd3 Nc6 8. Nd2 cxd4 9. exd4 Qb6 10. Nb3 a5 11. a4 d5! {муу. Хар давуутай. (Бондаревский - Болеславский, 1945)}) 7... e6 8. Nd2 {цагааны байрлал илүү аятайхан.}) 4. f3 Nd6 5. Nc3 c5! 6. dxc5 Nf5 7. Bf2 d4 {хүүний нөхөөст хар хүчтэй санаачлагатай. (Шерешевский - Тукмаков, 1981)}
Испани өрөг. Жишээ өргүүд II

  Нээгдсэн тоо: 1308 Төлбөртэй

c6 -гийн хар морийг цагаан тэмээгээр дарах эсхүл авах тогтмол заналхийхэд оршихын дээр зарим хувилбарт e5 хар хүүг сулруулах зорилготой тактик бол Испани өргийн санаа. Төрөл бүрийн шатрын програмууд гарааг цагаанд хамгийн ирээдүйтэйн нэг гэж үнэлэдэг. Өргийг их мастерууд тоглолтондоо өргөн ашиглахын дээр шатар сонирхогчдын дийлэнх нь энэ гараагаар ихээр тоглодог. Гарааны онолын хэсгийн хичээлүүдийг үзсэн бол одоо гарааг мастерууд өрөгтөө хэрхэн ашиглан тоглосон жишээнүүдийг үргэлжлүүлэн харцгаая.

Сайтын зарим материалуудыг үзэхийн тулд та тусгай эрхтэй хэрэглэгч байх ёстойг сануулъя. Өөрийгөө хөгжүүлэхэд багахан хэмжээний төлбөрөөс зайлсхийх хэрэггүй болов уу. Хүн өөрийгөө дайчлан суралцаж чаддаг болсны дараа л жинхэнэ сурах үйлс эхэлдэг гэдгийг ойлгоорой. Бие даан судалж сураагүй хүн олигтой мэдлэгтэй болно гэдэг юу л бол. Энэхүү хоосон зайг нөхөхөд сайтын зорилго оршиж байгаа болно.

[Event "Бильбао, 2009"] [White "Широв"] [Black "Аронян"] 1. e4 e5 2. Nf3 Nc6 3. Bb5 a6 4. Ba4 Nf6 5. O-O Be7 6. Re1 b5 7. Bb3 O-O 8. c3 d5 9. exd5 Nxd5 10. Nxe5 Nxe5 11. Rxe5 c6 12. d4 Bd6 13. Re1 Qh4 {харын идэвхижил өрсөлдөгчийн хүрээний сул нүднүүдтэй хослон цагаанд хүүний илүүгээ ашиглах боломжийг багасгасан} 14. g3 Qh3 15. Be3 Bg4 16. Qd3 Rae8 17. Nd2 Qh5 (17... Re6 {өөр зам боломжтой} 18. Qf1 Qh5 19. f3 Nxe3 20. Qf2 Nd5 21. fxg4 Qxg4 {гээд хар хангалттай тоглолттой. (Крамник - Аронян, Ереван, 2007)}) 18. a4 {угтсан тоглолтын стандарт арга.} ({Бакро - Аронын (Нальчик, 2009) нарын өрөгт цагаан} 18. Qf1 Re7 19. a4 Rfe8 20. axb5 axb5 21. Bxd5 Qxd5 22. Qg2 Qxg2+ 23. Kxg2 h5 24. Ra5 h4 25. Rea1 hxg3 26. hxg3 Be6 {гээд давууг олоогүй.}) 18... Re6 19. axb5 axb5 20. Nf1 Bf5 21. Qd2 Bh3 ({Иванчук - Соколов (Биль, 1989) нарын өрөгт хар} 21... Rfe8 22. Bxd5 cxd5 23. Bf4 Rxe1 24. Rxe1 Rxe1 25. Qxe1 Be4 26. Nd2 Bxf4 27. Nxe4 dxe4 28. gxf4 Qg4+ {гээд тоглолтыг тэнцвэржүүлсэн.}) 22. Bd1 Qg6 23. Bf3 Qf5 24. Bh1 Rfe8 25. Re2 h5 26. Qc2 Qg4 27. Ree1 h4 28. Qd1 Qf5 {энд хүртэл үйл явдал динамик тэнцвэрийн хүрээнд явагдсан ч цагаан илүү үр дүнд хүрэхээр шийдсэн.} 29. Qf3?? {ухаалаг өөр ямар нэгэн нүүдэл ийм үр дүнд авчрахгүй байсан байх} Qg6!! {цагаан буусан. Тэдэнд хамгаалалт байхгүй нь гайхмаар. Хар бэрсийг барих заналтай. Жишээ нь} 30. Ra6 ({хэрвээ} 30. Qd1 {гэвэл} hxg3 31. hxg3 Nxe3 {гээд цааш} 32. Rxe3 Rxe3 33. Nxe3 Rxe3! 34. fxe3 Qxg3+ {гэж бут ниргэнэ.}) 30... Bg4 31. Qg2 h3
Үйл явдал…

Үйл явдал /event/ тодорхой үйлдэл хийгдсэн талаар системд мэдэгддэг. Хэрвээ бид энэхүү үйлдлийг ажиглах хэрэгтэй бол яг энд…

Нээгдсэн тоо : 312

 
Холбоосын параметрүүд

Манай төсөл олон хуудсуудтай болон тэдгээрийн хооронд динамикаар шилжилт хийж байгаа ч тухайн үед шилжилт хийгдсэн хуудаст тохирох…

Нээгдсэн тоо : 410

 
Зочин (Visitor)

Зочин (Visitor) паттерн классуудыг өөрчлөхгүйгээр тэдгээрийн обьектуудын үйлдлийг тодорхойлох боломжийг олгоно. Зочин хэвийг ашиглахдаа классуудын хоёр ангилалыг тодорхойлно.…

Нээгдсэн тоо : 356

 
Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 452

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 528

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 524

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 628

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 725

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 761

 
Энэ долоо хоногт
Бодлого 2.110

илэрхийллийг хялбарчил.

Нээгдсэн тоо : 751

 
Бодлого 2.116

Нээгдсэн тоо : 809

 
Бодлого 8.122

Задаргааны сүүлээсээ 3 дахь гишүүний бином коэффициент 45 бол задаргааны 6-р гишүүнийг ол.

Нээгдсэн тоо : 661

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195