Функцын дифференциалчлал тасалдалгүй байдлын хоорондын холбоо
Ямар нэг цэг дээр f(x) функц нь дифференциалчлагдаж байвал тэр цэгт функц тасралтгүй байна. Эсрэгээсээ энэ нь буруу байдаг. Тасралтгүй функц нь уламжлалгүй байж болно.
Мөрдлөг. Хэрвээ функц нь ямар нэгэн цэг дээр тасарч байвал энэ цэг дээр функц нь уламжлалгүй.
Жишээ
y=|x| функц нь /Зур. 3/ тасралтгүй. Гэвч x=0 цэгт функцын график нь шүргэгчгүй тул уламжлал байхгүй.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




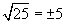 Учир нь (+5)2=25 бас (-5)2=25 байдаг.
Учир нь (+5)2=25 бас (-5)2=25 байдаг. 
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.