Олонлогийг латин цагаан толгойн том, элементийг жижиг үсгээр нь тэмдэглэдэг. 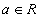 энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг
энэ бичлэг нь a нь R олонлогийн элемент ба энэ олонлогт харьяалагдана гэснийг илэрхийлнэ. Эсрэгээр a нь R олонлогт харьяалагдахгүй гэдгийг 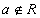 гэж бичнэ.
гэж бичнэ.
Хэрвээ A олонлогийн элемент бүр нь B олонлогт харьяалагддаг эсрэгээрээ B олонлогийн элемент бүр нь A олонлогт харьяалагддаг байвал эдгээрийг тэнцүү олонлогууд (A=B) гэнэ.
Хэрвээ A олонлогийн элемент бүр нь B олонлогт харьяалагддаг бол A олонлог нь B олонлогт багтсан эсвэл A олонлог нь B олонлогийн дэд олонлог гэж хэлдэг. /Зур. 1/ Энэ тохиолдлыг 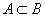 гэж бичнэ. Дурын A олонлогийн хувьд
гэж бичнэ. Дурын A олонлогийн хувьд 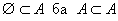 багтаалт хүчинтэй.
багтаалт хүчинтэй.
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэх




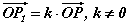 гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм.
гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.