Өмнөх хичээлийн жишээнүүдээс дүгнэн үзвэл захын хүүг бэрс гаргахад хамгаалж байгаа тал боломж ихтэй байсан. Тэгвэл илүү хүү нь захын биш байрлалтай бол байдал хэрхэн өөрчлөгдөх вэ? Хүчтэй тал өөрийн төлөвлөгөөг биелүүлж чадах уу? Захын хүүнүүд хичээлийн 2-р диаграмд хамгаалж байгаа талын ноён хүүний замд саад хийж чадахааргүй тохиолдолд асуудал амархан шийдэгдэж байсан. Тэгвэл хүүний давшиж байгаа босоо шугамд эсрэг ноён зогсож байгаа бол юу болох вэ? Дараах жишээнүүдээр дээрх асуултуудад хариулт өгөхийг оролдоё.
Юуны өмнө 1-р диаграмд анхаарна уу.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




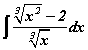 интеграл бод
интеграл бод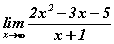 хязгаарыг бод.
хязгаарыг бод.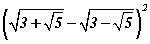 утгыг ол.
утгыг ол.