Хязгаарыг бодох аргууд сэдвээр дахин нэг хичээлийг танилцуулж байна. Энд бид хязгаарыг бодоход гайхамшигт хязгаарыг хэрхэн ашиглах талаар авч үзэх юм. Гайхамшигт хязгаар цөөн тооны байдаг ч оюутан сурагчдад ихэнхдээ нэг ба хоёрдугаар гайхамшигт хязгаарыг ашигладаг. ЕБС-ын хэмжээнд гайхамшигт хязгаарын талаар дэлгэрэнгүй үзээд байдаггүй ч эдгээрийг мэдэж байх нь зарим төрлийн бодлогыг бодолтонд маш хэрэгтэй болдог. Хичээлийг материалыг судлахаасаа өмнө Хязгаарыг ойлгох нь, Хязгаарыг бодох аргууд хичээлүүдийг үзэж судалсан байхыг сануулъя.
Нэгдүгээр гайхамшигт хязгаар
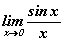 хязгаарыг аваад үзье. Хязгаарыг бодох аргууд хичээлд үзсэн аргын дагуу тэгийг илэрхийлэлд орлуулах гээд үзье. sin0=0 тэнцүү тул хүртвэрт тэг харин хуваар бол мэдээж тэг болно. Ингэснээр бид 0/0 тодорхойгүй байдалтай орлоо. Үүнийг яаж задлах вэ? Суут математикчдын баталсан нэгдүгээр гайхамшигт хязгаар нь биднийг ийм төрлийн тодорхойгүй байдлыг задлах ажлаас чөлөөлнө. Математик анализд
хязгаарыг аваад үзье. Хязгаарыг бодох аргууд хичээлд үзсэн аргын дагуу тэгийг илэрхийлэлд орлуулах гээд үзье. sin0=0 тэнцүү тул хүртвэрт тэг харин хуваар бол мэдээж тэг болно. Ингэснээр бид 0/0 тодорхойгүй байдалтай орлоо. Үүнийг яаж задлах вэ? Суут математикчдын баталсан нэгдүгээр гайхамшигт хязгаар нь биднийг ийм төрлийн тодорхойгүй байдлыг задлах ажлаас чөлөөлнө. Математик анализд 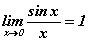 гэж баталдаг бөгөөд үүнийг нэгдүгээр гайхамшигт хязгаар гэдэг. Томьёоны баталгааг хийх нь өөр асуудал тул томьёог шууд цээжлээд аваарай. Бодлогуудад функцууд өөр байдлаар байрлаж болох ч энэ нь юуг өөрчлөхгүй. Жишээ нь
гэж баталдаг бөгөөд үүнийг нэгдүгээр гайхамшигт хязгаар гэдэг. Томьёоны баталгааг хийх нь өөр асуудал тул томьёог шууд цээжлээд аваарай. Бодлогуудад функцууд өөр байдлаар байрлаж болох ч энэ нь юуг өөрчлөхгүй. Жишээ нь 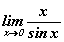 бол бас л 1-р гайхамшигт хязгаар.
бол бас л 1-р гайхамшигт хязгаар.
Санамж: Дур мэдэн хүртвэр хуваарийг хэзээ ч сольж болохгүй. Хязгаар 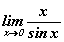 хэлбэрээр өгөгдсөн бол түүний юуг ч байрыг нь солихгүйгээр яг байгаа хэлбэрээр нь бодох ёстой.
хэлбэрээр өгөгдсөн бол түүний юуг ч байрыг нь солихгүйгээр яг байгаа хэлбэрээр нь бодох ёстой.
Практикт x-ийн оронд энгийн болоод нарийн төвөгтэй функцууд ч байж болно. Гэхдээ эдгээр нь зөвхөн тэг рүү тэмүүлж байх хэрэгтэй. Жишээ нь
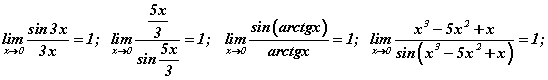
Энд 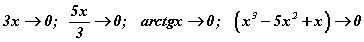 гээд бүгд тэг рүү тэмүүлж байгаа тул 1-р гайхамшигт хязгаарыг ашиглах боломжтой. Харин
гээд бүгд тэг рүү тэмүүлж байгаа тул 1-р гайхамшигт хязгаарыг ашиглах боломжтой. Харин 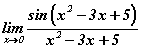 гэвэл бид 1-р гайхамшигт хязгаарыг ашиглаж болохгүй. Яагаад гэвэл x2-3x+5 олон гишүүнт тэг рүү биш 5 руу тэмүүлж байгаа анхаарна уу. Тэгэхлээр төстэй бичлэгтэй болгонд 1-р гайхамшигт хязгаарыг ашиглаад байж болохгүй, бас бодлого дээр авсан жишээнүүд байдлаар өгөгдөөд байдаггүйг санаж аваарай. Одоо 1-р гайхамшигт хязгаарыг ашиглах практик жишээнүүдийг авч үзье.
гэвэл бид 1-р гайхамшигт хязгаарыг ашиглаж болохгүй. Яагаад гэвэл x2-3x+5 олон гишүүнт тэг рүү биш 5 руу тэмүүлж байгаа анхаарна уу. Тэгэхлээр төстэй бичлэгтэй болгонд 1-р гайхамшигт хязгаарыг ашиглаад байж болохгүй, бас бодлого дээр авсан жишээнүүд байдлаар өгөгдөөд байдаггүйг санаж аваарай. Одоо 1-р гайхамшигт хязгаарыг ашиглах практик жишээнүүдийг авч үзье.
Бодлого 14.026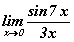 хязгаарыг бод.
хязгаарыг бод.
Бодлого 14.027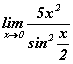 хязгаарыг бод.
хязгаарыг бод.
Бодлого 14.029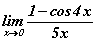 хязгаарыг бод.
хязгаарыг бод.
Бодлого 14.030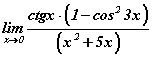 хязгаарыг бод.
хязгаарыг бод.
Дээрх жишээнүүдээс харвал 1-р гайхамшигт хязгаарыг ашиглан тригнометрийн функцууд агуулсан аймшигтай хязгааруудыг хөнгөн бодохоор байгаа тул хязгаарын энэхүү томьёог цээжлэн зэвсэглэлдээ аваарай.
Хоёрдугаар гайхамшигт хязгаар
Математик анализийн онолд 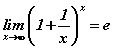 гэдгийг баталсан байдаг бөгөөд үүнийг хоёрдугаар гайхамшигт хязгаар гэдэг. e=2,718281828... - гэсэн иррационал тоо.
гэдгийг баталсан байдаг бөгөөд үүнийг хоёрдугаар гайхамшигт хязгаар гэдэг. e=2,718281828... - гэсэн иррационал тоо.
Практикт x-ийн оронд энгийн болоод нарийн төвөгтэй функцууд ч байж болно. Гэхдээ эдгээр нь зөвхөн хязгааргүй руу тэмүүлж байх хэрэгтэй. Томьёог шууд л цээжлэх хэрэгтэй.
Бодлого 14.031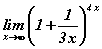 хязгаарыг бод.
хязгаарыг бод.
Хоёрдугаар гайхамшигт хязгаарын 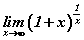 хувилбар бас байдаг. Үүнийг жишээгээр авч үзье.
хувилбар бас байдаг. Үүнийг жишээгээр авч үзье.
Бодлого 14.032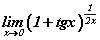
Дээрх жишээ нь бодлогод хоёр гайхамшигт хязгаарыг хоёуланг ашиглахыг харуулж байна. Хэдийгээр иймэрхүү төрлийн бодлогууд ерөнхий шалгалтанд ирэх магадлал багатай ч гайхамшигт хязгаарын шууд хэлбэрээр эсхүл маш бага хувиргалт хийсэн бодлого ирэх өндөр магадлалтай тул эдгээр хязгааруудыг мэдэх нь танд ашигтай.





 тэгшитгэлийг бод.
тэгшитгэлийг бод.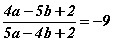 бол
бол 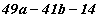 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.