Аравтын бутархай нь нэгжийг арав, зуу, мянга г.м хуваасны үр дүнд гарах хэсэг юм. Энэ бутархай нь бүхэл тооны бичлэгийн систем дээр үндэслэгдсэн тул тооцоолоход маш тохиромжтой. Иймээс аравтын бутархайн үйлдлүүд нь бүхэл тоон үйлдлүүдтэй бараг адилхан. Аравтын бутархайн бичлэгт хуваарийг бичих шаардлагагүй. Энэ нь тухайн тооны байрлалаар тодорхойлогдож байдаг. Бичлэг нь эхлээд тооны бүхэл хэсэг, дараа нь аравтын таслал тэгээд бутархай хэсэг. Аравтын таслалын дараагийн эхний тоо аравтын, хоёр дахь тоо нь зуутын, гурав дахь тоо нь мянгатын г.м заана. Аравтын таслалын дараа байрлах тоонуудыг аравтын орнууд гэнэ. Жишээ
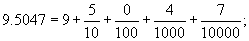
Аравтын бутархайн нэг давуу тал нь түүнийг маш амархан энгийн бутархайд шилжүүлж болдог.Аравтын таслалын ард байгаа тоо нь / жишээнээс 5047 / хүртвэр болно. Хуваарь нь 10 -ын n зэрэг байна. n нь аравтын орны тоотой тэнцүү. 9.5047 бутархайн хувьд n=4 байна. Тэгвэл
![]() гэсэн үг юм.
гэсэн үг юм.
Аравтын бутархай нь бүхэл хэсэггүй бол аравтын таслалын өмнө тэг тавина
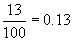
Аравтын бутархайн шинжүүд.
- Аравтын бутархайн ард тэгийг нэмж бичихэд утга нь өөрчлөгдөхгүй. 13.6=13.6000
- Аравтын бутархайн эцэст байгаа тэгийг устгахад утга нь өөрчлөгдөхгүй. 0.00123000=0.00123 Санамж. Эцэст нь биш тэгийг устгаж болохгүй
- Аравтын таслалын байрлалыг баруун тийш нь 1, 2, 3 г.м шилжүүлбэл бутархай 10, 100, 1000 г.м дахин өснө. 3.675 ---> 367.5 / бутархай 100 дахин өссөн энэ нь бутархайг 100 аар үржүүлсэнтэй адил/
- Аравтын таслалын байрлалыг зүүн тийш нь 1, 2, 3 г.м шилжүүлбэл бутархай 10, 100, 1000 г.м дахин буурна. 1536.78 ---> 1.53678 / бутархай 1000 дахин буурсан энэ нь бутархайг 1000 д хуваасантай адил/
Үелэх аравтын бутархай нь өөртөө давтагдасан төгсгөлгүй үргэлжлэх хэсэг буюу үеийг агуулж болно. Үеийг халтанд бичнэ.
Жишээ нь 0.12345123451234512345 ...=0.(12345). 47:11=4.27272727...=4.(27).





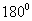 . Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно.
. Зөрсөн AB ба CD /Зур. 70/ хоёр шулууны хоорондын өнцгийг дараах байдлаар тодорхойлно. 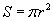 томьёогоор илэрхийлэгдэнэ; Хоёр хувьсагчийн функционал хамаарал хэсэгт авч үзсэн дээш шидэгдсэн биеийн хүрэх өндөр h, нийт хугацаа T хоёрын хамаарал гэх мэт. Агаарын эсэргүүцэл, дэлхийн таталтын хүч өндрөөс хамаардаг зэргийг тооцоогүй учраас энэ нь ойролцоо томьёо юм. Функционал хамааралыг томьёогоор илэрхийлэх боломжгүй эсвэл томьёо нь тооцоо хийхэд тохиромж муутай байх тохиолдол бас байдаг. Ийм үед функцыг хүснэгт эсвэл графикаар үзүүлдэг.
томьёогоор илэрхийлэгдэнэ; Хоёр хувьсагчийн функционал хамаарал хэсэгт авч үзсэн дээш шидэгдсэн биеийн хүрэх өндөр h, нийт хугацаа T хоёрын хамаарал гэх мэт. Агаарын эсэргүүцэл, дэлхийн таталтын хүч өндрөөс хамаардаг зэргийг тооцоогүй учраас энэ нь ойролцоо томьёо юм. Функционал хамааралыг томьёогоор илэрхийлэх боломжгүй эсвэл томьёо нь тооцоо хийхэд тохиромж муутай байх тохиолдол бас байдаг. Ийм үед функцыг хүснэгт эсвэл графикаар үзүүлдэг. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.