Бутархайг хувиргах

Аравтын бутархайг энгийн бутархай болгохдоо аравтын таслалын ардах тоог хүртвэр болгоод 10-ын n зэргийг хуваарь болгоно. n нь аравтын орны тоотой тэнцүү байна. Тэгээс ялгаатай бүхэл хэсэг нь хэвээрээ үлдэх бөгөөд тэг бүхлийг бичихгүй.

Жишээ

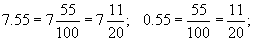
Энгийн бутархайг аравтын бутархай болгохдоо хүртвэрийг хуваарьт хуваана.

Жишээ 5/8 аравтын бутархай болго
Бодолт 5:8=0.625

Их олон тохиолдолд хуваах үйлдэл нь төгсгөлгүй үргэлжилдэг. Ийм тохиолдолд энгийн бутархайг аравтын бутархайд бүрэн хувиргах боломжгүй. Гэхдээ хуваах үйлдлээ хэрэгтэй гэсэн аравтын орныг гаргасны дараа зогсоодог.

Жишээ 1/3 аравтын бутархай болго
Бодолт 1:3=0.3333...

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Багтсан өнцөг

  Нээгдсэн тоо: 1719 Төлбөртэй

Математик ямар хэрэгтэй талаар хүмүүс олон янзаар ярьдаг. Зарим хүмүүс математикийн хэрэглээг зөвхөн 4 аргын тооны хүрээнд хардаг боловч өөрөө математикийн шинжлэх ухааны ололт дээр суурилан бий болсон техник хэрэгслүүдийг угаасаа байсан мэтээр хэрэглэж байдаг. Гэтэл зарим нэг хэсэг нь математикгүйгээр болоод л ирсэн гэсэн зүйлийг ч ярьж байдаг. Энэ бол хүмүүсийн ойлголтын өнцгүүд. Харин сайн сурдаг сурагчид бүгд математиктаа бусдаасаа илүү байдагийг бүгд мэднэ. Яагаад ийм зүй тогтол байдагт өөрийн бодлыг хэлье. Зарим хичээлд муу байж болох ч математикт муу байж болохгүй. Математикт сайн бол бусад хичээлд муу байх үндэсгүй гэдгийг баттай хэлэх байна. Иймээс хичээл сурлагадаа сайжран, амжилтанд хүрье гэвэл математикийн хичээлээ сайн үзэн ойлгоорой. Тэгвэл бусад хичээлүүдэд аяндаа сайн болоод ирнэ. Туршаад үзээрэй.

Энэ удаад тойрогт багтсан өнцгийн талаар авч үзье. Математикийг зөвхөн тоо бодох хүрээнд ердөө харж болохгүй. Онолын мэдлэгт суурилан асуудлын шийдлийг олдог юм шүү.

Зарим тодорхой интегралууд

  Нээгдсэн тоо: 5129 Нийтийн

Зарим тодорхой интегралууд



Паралель шулуун

  Нээгдсэн тоо: 19079 Нийтийн

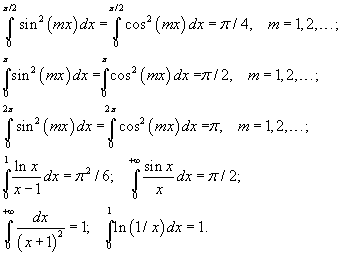
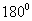Нэг хавтгай дээр орших хоорондоо огтлолцодгүй /Зур. 11/ AB ба CD шулуунуудыг паралель шулуун гэдэг бөгөөд AB || CD гэж тэмдэглэнэ. Паралель шугамын нэг дээр байрлах цэг нөгөө шугаман дээр байрлах цэгээс ижил зайд байна. Паралель шугамын хоорондох өнцөгийг тэг гэж үздэг. Нэг чигт чиглэсэн хоёр паралель цацрагийн хоорондох өнцөг тэгтэй , эсрэг чиглэлтэй тохиолдолд тэнцүү. KM шулуунтай перпендикуляр AB, CD, EF /Зур. 12/  шулуунууд нь өөр хоорондоо паралель байна. Паралель хоёр шулуунтай перпендикуляр шулууны урт нь паралель шулуунуудын хоорондын зай болно.

Магадлалын тодорхойлолт үндсэн шинжүүд

  Нээгдсэн тоо: 10478 Нийтийн

Магадлалын аксиом тодорхойлолт

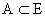Эгэл үзэгдлүүдийн олонлог E өгөгдсөн ба үзэгдэл бүрт :

  • P(A)≥0
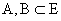  • хос харш үзэдлүүдийн хувьд:  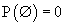тэнцэл биелнэ,
  • P(E)=1

харгалзсан цорын ганц P(A) тоо байна гэж үзье. Тэгвэл E олонлогийн үзэгдлүүдэд магадлал байна. P(A) тоог A үзэгдлийн магадлал гэж хэлнэ.

Үйл явдал…

Үйл явдал /event/ тодорхой үйлдэл хийгдсэн талаар системд мэдэгддэг. Хэрвээ бид энэхүү үйлдлийг ажиглах хэрэгтэй бол яг энд…

Нээгдсэн тоо : 292

 
Холбоосын параметрүүд

Манай төсөл олон хуудсуудтай болон тэдгээрийн хооронд динамикаар шилжилт хийж байгаа ч тухайн үед шилжилт хийгдсэн хуудаст тохирох…

Нээгдсэн тоо : 369

 
Зочин (Visitor)

Зочин (Visitor) паттерн классуудыг өөрчлөхгүйгээр тэдгээрийн обьектуудын үйлдлийг тодорхойлох боломжийг олгоно. Зочин хэвийг ашиглахдаа классуудын хоёр ангилалыг тодорхойлно.…

Нээгдсэн тоо : 339

 
Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 432

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 481

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 505

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 599

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 690

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 726

 
Энэ долоо хоногт
Бодлого 9.010

a ба b катеттай тэгш өнцөгт гурвалжин ерөнхий тэгш өнцөгтэй квадратыг багтаасан бол квадратын периметрийг ол.

Нээгдсэн тоо : 1133

 
Бодлого 15.055

функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.

Нээгдсэн тоо : 749

 
Бодлого 5.078

тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.

Нээгдсэн тоо : 820

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195