Интеграл тооцох бодлого сурагчид гэлтгүй оюутнуудад нилээд төвөг учруулдаг. Сэдэв математикийн хичээлдээ хүндэвтэрт ордогийн дээр практикт интегралыг үндсэн дөрвөн үйлдэл шиг тэр болгон хэрэглээд байдаггүйтэй холбоотой. Гэсэн хэдий ч ямарч шатны шалгалт шүүлэгт интегралын бодлого орохгүй байна гэдэг ховор. Интегралыг тооцох ерөнхий аргачлал бол интеграл доорх функцийг хувирган хүснэгтийн интегралын хэлбэрт оруулах. Хэрвээ интеграл доорх функц хүснэгтийн буюу шийдэгдсэн интегралын хэлбэрт орвол бодолт хийгдэнэ.
Хувиргалтыг буруу хийх, тохирох хүснэгтийн интеграл байхгүй бол интегралыг тооцох боломжгүй болно. ЕБС -ын сургуулийн хүрээнд маш цөөн тооны хүснэгтийн интегралыг ашигладаг ч эдгээрийг сурагчид тогтоосон байхыг шаарддаг. Би хувьдаа шалгалт шүүлэгт томьёоны хураамжийг ашиглахыг зөвшөөрөх нь зөв гэж боддог. Хүн маш олон тооны томьёо, чанаруудыг бүгдийг цээжээр мэдэх нь бараг боломжгүй бөгөөд шаардлагагүй зүйл. Харин тэдгээрийг хаана ямар байдлаар ашигладаг гэдгийг ойлгосон л байх хэрэгтэй.
ЕБС -ын хүрээнд ашигладаг хүснэгтийн интегралуудыг үзээрэй. Энэ удаад бутархайгаас интеграл тооцох аргуудыг авч үзье.
Юуны өмнө бутархайн интеграл гэдэг нь 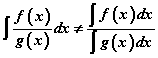 гэдгийг тогтоон аваараай. Өөрөөр хэлбэл бутархайн интеграл хүртвэрийн интегралыг хуваарийн интегралд хуваасантай тэнцүү биш гэсэн үг. Бутархайгаас интеграл авахад интеграл доорх функцээс хамаарсан хэдэн аргууд бий.
гэдгийг тогтоон аваараай. Өөрөөр хэлбэл бутархайн интеграл хүртвэрийн интегралыг хуваарийн интегралд хуваасантай тэнцүү биш гэсэн үг. Бутархайгаас интеграл авахад интеграл доорх функцээс хамаарсан хэдэн аргууд бий.
Арга I
Интеграл доорх функц зөв биш бутархайгаар илэрхийлэгдсэн хоёр олон гишүүнтийн харьцаа байх. Жишээ нь хүртвэрийн зэрэг хуваарийн зэргээс их эсхүл тэнцүү байх. Ийм тохиолдолд хүртвэрийн бүхэл хэсгийг ялгах эсхүл хуваарт буй илэрхийллээс хүртвэрийн илэрхийллийг салгах эсхүл хүртвэрийг хуваарт хуваах хэрэгтэй.
Жишээ
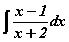 интегралыг тооц.
интегралыг тооц.
Сануулга. Хэрвээ хүртвэрт байгаа олон гишүүнтийн зэрэг хуваарийнхаас их байвал бүхэл хэсгийг салгахдаа хүртвэрийг хуваарт баганачлан хуваах нь илүү тохиромжтой.
Арга II
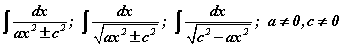 хэлбэрийн бутархайнуудад шинэ хувьсагч оруулах эсхүл тухайн интегралыг хүснэгтийн интегралд хувиргах аргуудыг хэрэглэдэг.
хэлбэрийн бутархайнуудад шинэ хувьсагч оруулах эсхүл тухайн интегралыг хүснэгтийн интегралд хувиргах аргуудыг хэрэглэдэг.
Жишээ
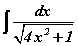 интегралыг бод.
интегралыг бод.
Арга III
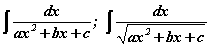 хэлбэрийн интегралуудыг хуваарт бүрэн квадратыг ялган хүснэгтийн интегралд шилжүүлэн боддог.
хэлбэрийн интегралуудыг хуваарт бүрэн квадратыг ялган хүснэгтийн интегралд шилжүүлэн боддог.
Жишээ
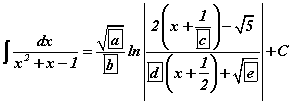 бол
бол 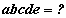
Бодолт
Жишээ ЭЕШ - 2018, D36
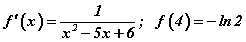 бол f(x) функцийг ол.
бол f(x) функцийг ол.
Арга IV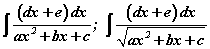 хэлбэрийн интегралуудад дараах аргачлалыг ашиглана. Хүртвэрээс хуваарийн уламжлалыг ялгаад дараа нь бутархайг гишүүнчлэн хуваавал нэгийнх нь хүртвэрт тогтмол харин нөгөөгийнх нь хүртвэрт хуваарийн уламжлал бүхий хоёр интегралын нийлбэр үүснэ. Тогтмол хүртвэртэй бутархайтай интегралыг III -р аргаар харин нөгөө интегралыг орлуулах аргаар олдог.
хэлбэрийн интегралуудад дараах аргачлалыг ашиглана. Хүртвэрээс хуваарийн уламжлалыг ялгаад дараа нь бутархайг гишүүнчлэн хуваавал нэгийнх нь хүртвэрт тогтмол харин нөгөөгийнх нь хүртвэрт хуваарийн уламжлал бүхий хоёр интегралын нийлбэр үүснэ. Тогтмол хүртвэртэй бутархайтай интегралыг III -р аргаар харин нөгөө интегралыг орлуулах аргаар олдог.
Жишээ
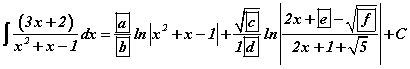 бол a+b+c+d+e+f=?
бол a+b+c+d+e+f=?
Бодолт
Бодлого бодох аргуудыг сайн эзэмшсэн байхад ямарч бодлогыг цаг алдахгүй хурдан шийдэх боломжтой тул онолын мэдлэгээ зузаатгаж байхыг зөвлөе.





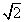
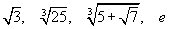
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.