Дөрвөн морины гараа нь XVI -р зууны Полериогийн гар бичмэлүүдэд анхны судалгаанууд байдаг эртний гараануудын нэг. Гарааны боловсруулалтад Л. Паульсен, А. Рубинштейн, Ф. Маршалл нар их хувь нэмэр оруулсан. Гараагаар Э. Ласкер, Х. Р. Капабланка, М. Ботвинник зэрэг дэлхийн аваргууд өрөгтөө нэг бус удаа тоглосон байдаг. Гараанд байрлалын тайван тоглолтонд хүргэдэг симметр системийн зэрэгцээ хурц үргэлжлэлийг ч боловсруулсан. Өнөө үед тоглолтод гараа ховор харагдах болсон.
Шатарыг боломжийн хэмжээнд цаашлаад тамирчны зэрэгт хүрч сурахаар хичээж байгаа хүмүүс гарааны онолыг мэдэн судлах зайлшгүй шаардлагатай. Сонирхогчдын тухайд бол гарааны арваад нүүдэлд аль нэг нь алдаа хийснээр тоглолтын хувь заяа шийдэгдэх нь элбэг байдаг. Энэ нь сонирхогчид гарааны онолд нэг их ач холбогдол өгдөггүйтэй холбоотой. Хэрвээ та сайтад тавигдаж байгаа шатрын гараануудын хичээлүүдийг сайтар ойлгон судалбал жирийн нэгэн сонирхогчоос өөр түвшинд хүрнэ гэдэгт итгээрэй.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
тэгшитгэлийг бод.
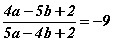бол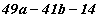 
илэрхийллийн утгыг ол.