Гроссмейстерүүд өрөгтөө хамгийн өргөн ашигладаг гараануудын нэг бол Испани өрөг. Гарааг зохиогчийг Руи Лопес гэж үздэг. Зарим улсуудад гарааг зохиогчийн нэрээр буюу "Руи Лопесийн /Ruy Lopez/ гараа" гэж нэрлэдэг. Гэсэн хэдий ч энэхүү гарааны талаарх анхны мэдээлэл XV-XVI зууны Испаний шатарчин Луис Рамирес де Лусений гарын авлагад дурдагдсан байдаг. Гараа нь нарийн, олон төрлийн схемтэйгээрээ онцлогтой. Гарааны онолын боловсруулалтад В. Стейниц, К. Яниш, М. Чигорин, Ф. Маршалл, З. Тарраш, А. Алехин, М. Эйве, П. Керес, В. Смыслов, И. Болеславский, И. Зайцев, С. Фурман, А. Карпов, Г. Каспаров, Г. Липский зэрэг олон тооны шатарчид их үүрэг гүйцэтгэсэн.
Испани өргийн санаа нь c6 -гийн хар морийг цагаан тэмээгээр дарах эсхүл авах тогтмол заналхийхэд оршихын дээр зарим хувилбарт e5 хар хүүг сулруулах зорилготой. Төрөл бүрийн шатрын програмууд гарааг цагаанд хамгийн ирээдүйтэйн нэг гэж үнэлэдэг.
Шатар сонирхогч болон суралцагчид шатрын гарааны мэдлэгээ дээшлүүлэх нь тоглолтын чанарт илт мэдэгдхүйц дэвшил авчирдаг. Иймд сайтад нийтлэгдэж буй гарааны хичээлүүдийг уншин судлаарай.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




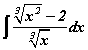 интеграл бод
интеграл бод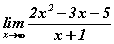 хязгаарыг бод.
хязгаарыг бод.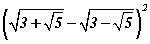 утгыг ол.
утгыг ол.