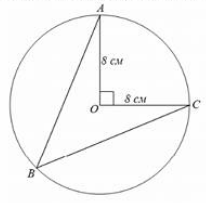
 O төвтэй тойргийн радиус нь 8 см. AOC өнцөг нь 900. AB=BC бол
O төвтэй тойргийн радиус нь 8 см. AOC өнцөг нь 900. AB=BC бол
- AC -ийн урт
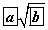
- ABC өнцөг
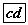
- BC -гийн урт
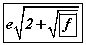
байна.
Бодолт
- AC цэгийг холбовол 8 см урттай катетуудтай AOC тэгш өнцөгт гурвалжин үүснэ. AC нь AOC тэгш өнцөгт гурвалжингийн гипотенуз тул Пифагорын теоремоор
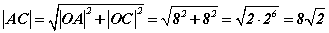 гэж гарах тул a=8; b=2 болно.
гэж гарах тул a=8; b=2 болно. - AOC төв өнцөг харин ABC багтсан өнцөг гэдгийг мэдэж байвал багтсан өнцгийн хэмжээ тухайн нумд тулгуурлсан төв өнцгийн хагастай тэнцүү теоремоор ABC =450 гэдгийг амархан олно. Иймээс c=4; d=5 байна. Тойргийн элементүүд хичээлийг үзээрэй. Теоремийг мэдэхгүй бол AOC төв өнцгийг 360-90=270 градус гэж үзэж болно AB=BC нөхцлөөр ABO, OBC гурвалжингууд тэнцүү гэдгээс BOC өнцөг 135 градус харин OBC гурвалжингийн суурийн өнцгүүд 180-135=45/2 гэдгийг олно. Эндээс AOC=2·(180-135)/2=45 гэдгийг амархан тооцно.
- Тойргийн радиус болох BO хэрчмийг татвал AB=BC нөхцлөөр ABO, OBC гурвалжингууд тэнцүү байж таарна. AOC төв өнцгийг 360-90=270 градус гэж үзэж бас болно. ABO, OBC гурвалжингууд тэнцүү гэдгээс BOC өнцөг 135 градус байхын дээр |BO|=|OC|=8см тул косинусын
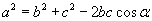 теоремоор
теоремоор 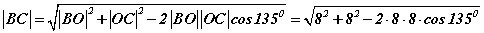 байна. Тооцоог хийвэл
байна. Тооцоог хийвэл 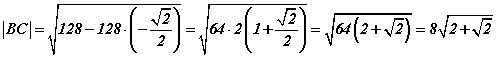 гэж гарна. Эндээс e=8; f=2 байна.
гэж гарна. Эндээс e=8; f=2 байна.
Хариу
a=8; b=2; c=4; d=5; e=8; f=2;





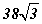 талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.
талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.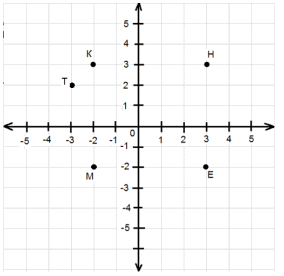 Тэгш өнцөгт координатын хавтгайд 5 цэг өгөв.
Тэгш өнцөгт координатын хавтгайд 5 цэг өгөв.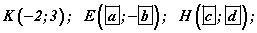
 цэг орохгүй.
цэг орохгүй. илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.