Координатийн хавтгайд A(-5, -2), B(5, 4), C(2, a) гурван цэг нэг шулуун дээр байх бол a тоог ол.
Бодолт
y=kx+b томьёогоор өгөгдсөн функцийг шугаман функц гэдэг бөгөөд функцийн график шулуун байдаг. Тэгвэл A(-5, -2), B(5, 4) цэгүүдийн хувьд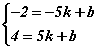 
систем үүснэ. Цэгийн координат M(x; y) байдлаар өгөгддөг гэдгээс y=kx+b томьёонд A(-5, -2), B(5, 4) цэгүүдийн координатийг тавиад систем үүсч байгаа юм. Системийн тэгшитгэлүүдийг нэмэхэд үүсэх 2b=2 тэгшитгэлээс b=1 гэж гарна. b=1 -ийг системийн аль нэг тэгшитгэлд тавин тооцвол 4=5k+1 -ээс k=3/5 гэж гарна. Эндээс гурван цэгийг агуулах шулууны тэгшитгэл 
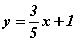байх бөгөөд тэгшитгэлд C(2, a) цэгийн координатийг оруулан тооцвол 
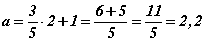гарна.
Зөвлөмж:
- Ямарч бодлогын бодолтод онолын нэг болон түүнээс дээш ухагдхуун ашигладана. Энэ бодлогын тухайд шугаман буюу шулууны томьёог мэдэж байж л асуудлыг шийднэ. Иймээс сайтын математик математик хэсгийн хичээлүүдтэй сайтар танилцахыг зөвлөе.
- Бодлогыг бүр дийлэхгүйд хүрвэл координатийн хавтгайд A(-5, -2), B(5, 4) цэгүүдийг тэмдэглээд тэдгээрийг дайрсан a шулуун татаад C цэгийн X тэнхлэгийн координат 2 -ийг дайрсан X тэнхлэгтэй перпендикуляр шулууныг татан a шулуунтай огтлолцсон цэгийн Y тэнхлэг дээр утгаар хариуг баримжаалж болох юм.
Хариу
2,2
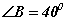бөгөөд AM=BM байхаар M цэгийг BC хажуу тал дээр авсан бол 
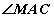өнцгийг ол.
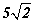диагоналтай квадратын талыг ол.
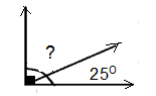Мэдэгдэхгүй байгаа өнцгийн хэмжээг олоорой.
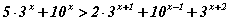тэнцэтгэл бишийг бод.
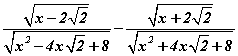илэрхийллийн x=3 утгыг ол.