Тоон дараалал
Натурал тоон цувааг авч үзье.
1, 2, 3, … ,n-1, n, …
Энэ цувааны тоо бүрийг тодорхой дүрмийн дагуу ямар нэгэн un тоогоор соливол шинэ тоон цуваа үүснэ.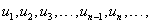 тэмдэглэгээ
тэмдэглэгээ 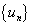
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэхТоон дараалал
Натурал тоон цувааг авч үзье.
1, 2, 3, … ,n-1, n, …
Энэ цувааны тоо бүрийг тодорхой дүрмийн дагуу ямар нэгэн un тоогоор соливол шинэ тоон цуваа үүснэ.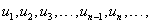 тэмдэглэгээ
тэмдэглэгээ 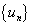
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэхМэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.