Нимцович өөрийн санааг илэрхийлж байх тэр үед түүний тэргээр хийсэн нүүдлийг "нууцлаг" хэмээн шоглонгуй нэрлэж байсан шүүмжлэгчид байсанг номондоо дурджээ. Ийм төрлийн нүүдлийг дараах байрлалаас харцгаая. Блекберн - Нимцович. Петербург, 1914
Блекберн - Нимцович. Петербург, 1914
Цагааны 14 дэх нүүдлийн дараа үүссэн байрлал. Хар тэргээр f8 аас e8 -д нууцлаг нүүдлийг хийсэн. Энэхүү нүүдлийг боломжит d3-d4 урагшлалтын эсэргүүцэн сонгосон. Цагаан тохиромжтой үе гарахад л d3-d4 гэж тоглох санаатай. Трf8-e8 шилжилт энэхүү чөлөөлөгдөх нүүдлийг хүндрүүлэх зорилготой. Иймээс тэрэгний нүүдэл урьдчилсан арга хэмжээ маягийн болж ирнэ. "Нууцлаг" гэдэг нь гадаад хэлбэр талаасаа тэрэг одоохондоо хаалттай шугамыг эзлэж байгаа болохоос түүний стратегийн зорилго ерөөсөө биш. Шатруудаар зөвхөн дайралтын нүүдэл хийхийг оролдох нь дундаж тоглогчийн түвшин. Тоглолтыг илүү нарийн ойлгох тусам шатруудаар урьдчилсан ажиллагаа хийхийг оролдох нь бүрэн үндэслэлтэй. Үйл явцын ердийн явцыг тайлбарлая. Ихэнх тохиолдолд хүүний урагшлалтаар хэрэгждэг өрсөлдөгчийн чөлөөлөгдөх маневр үр дүндээ нээлттэй шугамыг бий болгодог. Иймээс бидний мэдэлд байхгүй ч ирээдүйд бий болох шугамыг бид урьдчилан эзлэн өрсөлдөгчид чөлөөлөгдөх маневр явуулахад нь хүндрэл үүсгэх юм. Тэрэгний "нууцлаг" нүүдэл бол ухаалаг стратегийн бүрдүүлэгч хэсэг. Тэрэгнүүд хамгийн идэвхитэй байрлалыг эзлэх ёстой гэсэн өргөн тархсан үзэл байдгийг дурдаад Нимцович тухайн үед тэрэг идэвхитэй ажиллаж байна уу эсхүл идэвхигүй байрлал эзэлсэн гэдгээс өрсөлдөгчийн чөлөөлөгдөх нүүдлийг анхаарах нь хамаагүй илүү гэдгийг батлана гэжээ.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




 тэгшитгэлийг бод.
тэгшитгэлийг бод.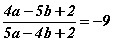 бол
бол 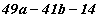 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.