Бодлогыг олон янзаар бодох аргуудыг эзэмших нь бодлого бодох техникт маш сайнаар нөлөөлөн ямарч бодлогыг өөр өнцгөөс харан шийдлийн олон санааг төрүүлдэг тул энэ удаад 3x2+7x-10=0 тэгшитгэлийг бодох аргуудыг авч үзье. Тэгшитгэлийн коэффициентүүдийг 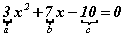 a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.
a - квадрат зэрэгтэй гишүүний, b - нэгдүгээр эрэмбийн гишүүний , c - сул гишүүн гэж тэмдэглэе.
Уламжлалт дискриминантаар бодох арга.
Квадрат тэгшитгэлийн дискриминантийг олох 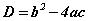 томьёогоор
томьёогоор 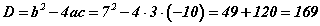 гэж гарна. Дискриминант эерэг тоо учраас квадрат тэгшитгэл хоёр шийдтэй. Квадрат тэгшитгэлийн шийдийг олдог
гэж гарна. Дискриминант эерэг тоо учраас квадрат тэгшитгэл хоёр шийдтэй. Квадрат тэгшитгэлийн шийдийг олдог 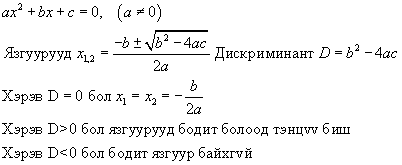 томьёоны дагуу тэгшитгэл
томьёоны дагуу тэгшитгэл 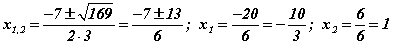 шийдүүдтэй гэж гарна.
шийдүүдтэй гэж гарна.
Коэффициентийн нийлбэрээр олох арга.
Тэгшитгэлийн коэффициентүүдийн нийлбэрийг олъё. Анхдагч тэгшитгэлээс x -ийг хасвал 3+7-10=0 гэсэн адитгал гарна. Коэффициентүүдийн нийлбэрийн нийлбэрийн аргад тэгшитгэлийн коэффициентүүдийн нийлбэр тэгтэй тэнцүү бол тэгшитгэлийн нэг шийд 1 харин нөгөө шийд c/a -тай тэнцүү байдаг гэдгээс x1=1; x2=-10/3 гэж гарна.
Виетийн теоремоор бодох
Тэгшитгэлийг Виетийн теоремоор бодохын тулд тэгшитгэлийн хоёр талыг x2 гишүүний коэффициентод хуваан эмхэтгэсэн тэгшитгэлийн 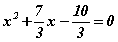 хэлбэрт оруулъя.
хэлбэрт оруулъя. 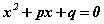 хэлбэрийн эмхэтгэсэн тэгшитгэлийн хувьд Виетийн теоремоор
хэлбэрийн эмхэтгэсэн тэгшитгэлийн хувьд Виетийн теоремоор 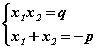 систем биелэх ёстой. ЕБС -д Виетийн теоремийн системд тэгшитгэлүүдийн байрыг сольж заагаад байдаг. Эхлээд үржвэрийг хангах шийдүүдийг сонгох нь амар байдаг тул системийн эхний тэгшитгэлд үржвэр байдгаар тогтоовол илүү. Манай тэгшитгэлийн хувьд -10/3 утгыг өгөх хамгийн энгийн тоонууд бол 1 ба -10/3 юм. Эдгээр тоог хоёрдугаар тэгшитгэлд тавин шалгавал 1-10/3=-7/3 гэж -p гарч ирснээр тэгшитгэл x1=1; x2=-10/3 шийдтэй нь батлагдлаа.
систем биелэх ёстой. ЕБС -д Виетийн теоремийн системд тэгшитгэлүүдийн байрыг сольж заагаад байдаг. Эхлээд үржвэрийг хангах шийдүүдийг сонгох нь амар байдаг тул системийн эхний тэгшитгэлд үржвэр байдгаар тогтоовол илүү. Манай тэгшитгэлийн хувьд -10/3 утгыг өгөх хамгийн энгийн тоонууд бол 1 ба -10/3 юм. Эдгээр тоог хоёрдугаар тэгшитгэлд тавин шалгавал 1-10/3=-7/3 гэж -p гарч ирснээр тэгшитгэл x1=1; x2=-10/3 шийдтэй нь батлагдлаа.
Шилжүүлэх аргаар бодох
Шилжүүлэх аргад x2 гишүүний коэффициентийг сул гишүүнд шилжүүлэн үржүүлэн туслах тэгшитгэлийг гаргадаг. Тэгвэл анхдагч тэгшитгэлээс 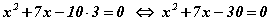 гэсэн туслах тэгшитгэл гарч ирнэ. Сүүлийн тэгшитгэлийн шийдийг Виетийн теоремоор олвол үржвэр нь -30 харин нийлбэр нь -7 буюу 1 -р эрэмбийн гишүүний коэффициентийг сөрөг тэмдэгтэй авсантай ижил утгууд өгөх -10, 3 тоонууд байна. Туслах тэгшитгэлийн шийдээс анхдагч тэгшитгэлийн шийдийг олохдоо шийдүүдийг анхдагч тэгшитгэлийн x2 гишүүнээс шилжүүлсэн коэффициентод хуваадаг тул x1=1; x2=-10/3 шийдүүд гарна.
гэсэн туслах тэгшитгэл гарч ирнэ. Сүүлийн тэгшитгэлийн шийдийг Виетийн теоремоор олвол үржвэр нь -30 харин нийлбэр нь -7 буюу 1 -р эрэмбийн гишүүний коэффициентийг сөрөг тэмдэгтэй авсантай ижил утгууд өгөх -10, 3 тоонууд байна. Туслах тэгшитгэлийн шийдээс анхдагч тэгшитгэлийн шийдийг олохдоо шийдүүдийг анхдагч тэгшитгэлийн x2 гишүүнээс шилжүүлсэн коэффициентод хуваадаг тул x1=1; x2=-10/3 шийдүүд гарна.
Бүрэн квадратийг ялгах арга
Тэгшитгэлээс бүрэн квадратыг ялгахын тулд тэгшитгэлийн хоёр талыг x2 гишүүний коэффициентод хуваан эмхэтгэсэн тэгшитгэлийн 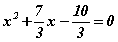 хэлбэрт оруулъя. 1 -р эрэмбийн үл мэдэгчийн коэффициент эерэг учраас нийлбэрийн квадратыг
хэлбэрт оруулъя. 1 -р эрэмбийн үл мэдэгчийн коэффициент эерэг учраас нийлбэрийн квадратыг 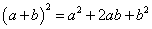 ялгах гэж оролдох хэрэгтэй. Хэрвээ коэффициент сөрөг байсан бол ялгаварын квадратыг ялгах гэж оролдох нь зүйн хэрэг. Тэгшитгэлийн x2 бол a2 -тай ижил тул эхний гишүүн бэлэн гэсэн үг. Задаргааны 2ab гишүүний a бол x харин бидэнд 2 болон b байхгүй. Тэгшитгэлийн хоёрдугаар гишүүнийг 2 -оор үржүүлээд 2 -т хуваавал
ялгах гэж оролдох хэрэгтэй. Хэрвээ коэффициент сөрөг байсан бол ялгаварын квадратыг ялгах гэж оролдох нь зүйн хэрэг. Тэгшитгэлийн x2 бол a2 -тай ижил тул эхний гишүүн бэлэн гэсэн үг. Задаргааны 2ab гишүүний a бол x харин бидэнд 2 болон b байхгүй. Тэгшитгэлийн хоёрдугаар гишүүнийг 2 -оор үржүүлээд 2 -т хуваавал 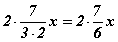 болно. Эндээс 2x бол 2a тул b=7/6 болж таарна. Бүрэн квадрат гарч ирэхэд b2 дутуу тул түүнийг тэгшитгэлд нэмээд, хасвал
болно. Эндээс 2x бол 2a тул b=7/6 болж таарна. Бүрэн квадрат гарч ирэхэд b2 дутуу тул түүнийг тэгшитгэлд нэмээд, хасвал 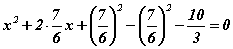 болно. Тэгшитгэлийн эхний гурван гишүүн
болно. Тэгшитгэлийн эхний гурван гишүүн 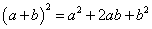 томьёо гэдгээс тэгшитгэлд хувиргалтыг хийвэл
томьёо гэдгээс тэгшитгэлд хувиргалтыг хийвэл
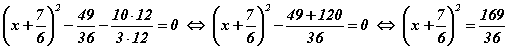 болно. Квадрат язгуур аваад шийдийг олвол
болно. Квадрат язгуур аваад шийдийг олвол  гэж гарна. Бүрэн квдрат ялгах аргаар тэгшитгэлийг бодох нь арай ажиллагаа ихтэй боловч илэрхийллийг хувирган эмхэтгэхэд голлон хэрэглэдэг аргачлал тул квадрат ялгаж байгаа техникийг сайн ойлгон тогтоон авахыг зөвлөе.
гэж гарна. Бүрэн квдрат ялгах аргаар тэгшитгэлийг бодох нь арай ажиллагаа ихтэй боловч илэрхийллийг хувирган эмхэтгэхэд голлон хэрэглэдэг аргачлал тул квадрат ялгаж байгаа техникийг сайн ойлгон тогтоон авахыг зөвлөе.





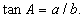 олох юм.
олох юм.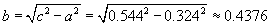 Өнцөг нь
Өнцөг нь 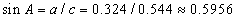 буюу
буюу 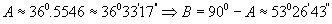 болно.
болно.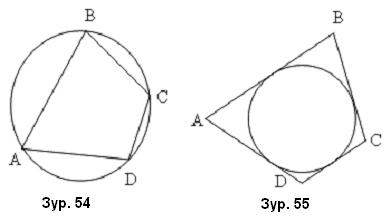
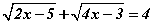 тэгшитгэл бод.
тэгшитгэл бод.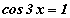 тэгшитгэл бод.
тэгшитгэл бод.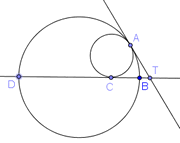 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.