Шатарт тодорхой байрлалаас өрсөлдөгчид мад өгөх аргыг сайн мэддэг, түүнийг ашиглаж сурахад шатрын бодлого сайн туслагч. Гурван нүүдлийн мадны бодлогын шийдлийг олж чадаж байвал та гурван нүүдлийн тооцоог хийж чадаж байна гэсэн үг. Байрлал болоод хүчний давуу болж ирэхэд хайнга тоглон стандарт мадны байрлалыг харалгүй өнгөрч улмаар бүр хожигдох ч тохиолдол гардаг. Иймд шатрын бодлогуудыг шийдэн тоглолтын чадвараа байнга дээшлүүлж байгаарай.
Шатарын нүүдлийг ойлгон нүүж сурах тийм ч хэцүү зүйл биш. Бага насны хүүхэд ч ердөө сарын дотор нүүгээд сурчихна. Харин шатар тоглож сурна гэдэг хүндхэн болоод ихээхэн хүч хөдөлмөр шаардсан ажил. Ямарч зүйлийг дадлагагүйгээр сурахад хэцүү тул сайтын энэхүү буланд шатрын бодлого, этюд, тоглолтын татктикийн шийдлийг олох гэх мэтийн асуудлыг хамарсан материалуудыг нийтлэх болно.
Шатарт тодорхой байрлалаас өрсөлдөгчид мад өгөх аргыг сайн олж харж чадаж байвал их хэрэгтэй. Нэг нүүдлийн мадыг хүмүүс хэтэрхий амархан гэж үзээд бараг тоохгүй байдаг ч яг тоглолтын явцад нэг нүүдлийн мадыг харалгүй өнгөрөн цаашид хожигдолд хүрэх нь элбэг байдаг. Юмыг багаас нь сурч эхлэх бол хууль учраас бодлогуудыг бодон дадлагажаарай.
Шатарт тодорхой байрлалаас өрсөлдөгчид мад өгөх аргыг сайн олж харж чадаж байвал их хэрэгтэй. Хоёр нүүдлийн мадыг олон харж чадаж байвал та шатар тоглож сурч байна гэсэн үг. Энгийн байрлалд хоёр нүдний мадыг амархан шийдэх ч хөлөг дээр олон шатрууд байх үед бодлого бас тийм амарханд орохгүй шүү.
Сайтын энэ хэсэгт дөрвөн нүүдлээр мад өгөх шатрын бодлогуудыг нийтлэнэ. Тоглолтын явцад дөрвөн нүүдлийг тооцон харна гэдэг амаргүй. Мэрэгжлийн шатарчид үүнийг төвөггүй хийх боловч эхлэн суралцагч, сонирхогчдод энэ ажил тийм ч амар биш. Иймээс дөрвөн нүүдлээр мад өгөх бодлогуудын шийдлийг олж сурвал тоглох ур чадварт гарцаагүй сайн нөлөө үзүүлнэ.
Шатрын бодлогуудаас гадна шатар тоглох чадварыг дээшлүүлэх бас нэгэн сайн хэрэгсэл бол байрлалаас зөв үргэлжлэлийг олох юм. Заавал мад өгөхгүйгээр хожлыг олох, хүнд байдлаас гарах гэх мэтээр олон тохиолдолууд байж болно. Эдгээр нь практикт бодлогоос илүү тохиолддог тул сайн судлан мэддэг болсон байх хэрэгтэй.
длогуудыг нийтлэнэ. Олон нүүдлийн бодлогууд эхлэн суралцагчдад төвөгтэй байж мэдэх учраас нэгтгэн нэг хэсэг болгосон. Олон нүүдлийн комбинаци олон төрлийн хувилбаруудтай байх тул бодлогууд тийм ч амар шийдэлгүй байж мэднэ.





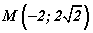 цэгээс координатийн эх хүртлэх зайг олоорой.
цэгээс координатийн эх хүртлэх зайг олоорой.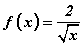 функцийн хувьд f'(4) -ийн утгыг олоорой.
функцийн хувьд f'(4) -ийн утгыг олоорой.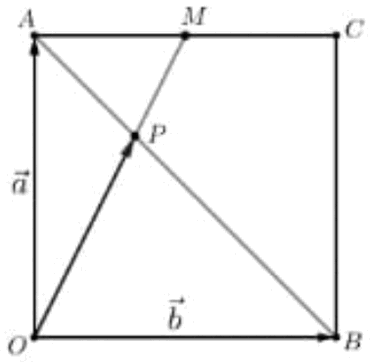 OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв
OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв 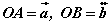 бол
бол 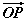 -ийг
-ийг 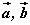 -ээр илэрхийл.
-ээр илэрхийл.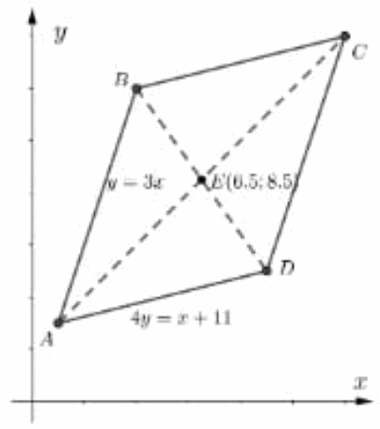 ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой.
ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой. AB диаметр ба
AB диаметр ба 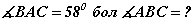 .
.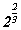 зэргийг язгуур хэрэглэн бичээрэй.
зэргийг язгуур хэрэглэн бичээрэй.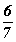 тооны урвуу тоог олоорой.
тооны урвуу тоог олоорой.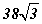 талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.
талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.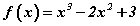 функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.
функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.