Тригнометрийн хувиргалтын бодлогуудыг сайн ойлгон эзэмшиж сурснаар тригнометрийн тэгшитгэлүүдийг бодох үндэс болно. Тригнометрийн хувиргалтуудад олон тооны томьёонуудыг ашиглахаас гадна алгебрын хувиргалтуудад ашигладаг томьёонуудыг ч давхар ашигладаг тул эхлээд жаахан хүндхэн мэт санагдаж магадгүй. Үндсэн функцуудын тодорхойлолт, геометр утгыг ойлгосон байх нь их чухал.
Ерөнхий шалгалтанд математикийн хичээлээр хүчээ сорих гэж буй хүүхэд багачуудад зориулан энэхүү хэсгийг нээж байгаа юм. Төгсөлтийн, ерөнхий, элсэлтийн шалгалтанд ирж байсан болон бодлого бодох ерөнхий зарчмуудыг ойлгоход тусламж болохоор төрөл бүрийн сэдвээр бодлогууд тавигдах болно.
Тригнометрийн тэгшитгэлүүдийг бодоход хамгийн чухал хэсэг нь энгийн тэгшитгэлүүдийн шийдийг цээжилсэн байх явдал юм. Тригнометрийн ихэнх тэгшитгэлийг зохих хувиргалтуудыг хийн энгийн тэгшитгэлд шилжүүлэн боддог тул энгийн тэгшитгэлийн шийдийг заавал мэдэж байх хэрэгтэй. Үүнээс гадна тригнометрийн функцууд үелэх функцууд гэдгийг байнга санаж байх хэрэгтэй.
Математикийн бодлогуудыг бодох үедээ сурагчдын гаргадаг түгээмэл алдаануудын нэг бол тухайн функцын утгын болоод тодорхойлогдох мужийг зөв тооцоогүйтэй холбоотой байдаг. Бүхий л тэгшитгэл, тэнцэл биш, илэрхийлэл зэргийг бодохдоо тэдгээрийн утгын болоод тодорхойлогдох мужийг заавал тооцсон байх шаардлагатай.
Хязгаартай холбоотой бодлогууд нилээд асуудал үүсгэдэг. Учир нь эндээс математик анализын эхлэл тавигдаж байгаа болохоор сэдэв хүндэвтэр. Гэхдээ ерөнхий боловсролын программд сэдвийг эхлэлийн шатанд үздэг тул ерөнхий ойлголтоо сайн ойлгосон байхад бодлогуудыг их хүндрэлгүй бодох боломжтой.
Уламжлал бол анализын эхлэл хэсэгт багтана. Сэдвийн бодлогуудыг бодоход энгийн функцуудын уламжлалыг заавал мэдэх хэрэгтэй. Геометр утгыг сайн ойлгоод, энгийн функцуудын уламжлалыг мэдэж байвал бусад хэсэг нь илэрхийлэл хялбарчлах, адитгал хувиргалтуудтай төстэй техникээр бодлогыг боддог.
Уламжлал, интеграл бол анализын эхлэлийн сэдвүүд. Онолын хэсгийн материалуудыг сайн ойлговол эдгээр нь зэрэг дэвшүүлэх, язгуур гэх мэтийн эсрэг үйлдлүүдтэй ижилхэн үйлдлүүд юм. Бодлогууд энгийн байдаг болохоор зохих дүрмээр хувиргалт хийгээд үндсэн интегралууд руу шилжүүлээд боддог.
Ерөнхий, анги дэвших, явцын шалгалтуудад ийм төрлийн бодлого орж ирэх нь бараг л хууль. Энд маш өргөн хүрээтэй бидний амьдралд өдөр бүр тохиолдох бодлогууд багтдаг тул ийм төрлийн бодлогуудыг заавал бодож сурах хэрэгтэй. Хурд, хольц, хувь хөнгөлөлт, урсгалын бодлогууд бараг бүхий л шалгалт, шүүлэг, сорилгод багтсан байдаг.
Логикийн бодлогууд хүмүүс өөрийгөө хөгжүүлэхэд илүү тустай. Ялангуяа гэр бүл эсхүл найз нөхдүүд хамтран ямар нэгэн зүй тогтолыг олох, таавар, стандарт бус бодлогын шийдлийг гаргах нь сонирхолтой ажил. Математикийн бодлогууд цэвэр техник, аргачлалыг түлхүү шаарддаг бол логикийн бодлогууд амьдралд илүү ойр, таниас гоц гойд мэдлэг шаардахгүй ч хүний ялангуяа хүүхдийн сэтгэн бодох чадварыг дээшлүүлэхэд маш үр дүнтэй.
Математик статистикийг өгөгдөл цуглуулан боловсруулалт хийн шинжлэх ухаааны болон практик дүгнэлтийг гаргах зорилготой математикийн ухааны нэг бүлэг гэж үздэг. Математик статистик нь бодит амьдралд математик хэрэглээний салбарлалт тул сонирхолтой бөгөөд практик ач холбогдолтой. ЕБС -д математик статистикийн суурь ухагдхуунуудыг заадаг ч энэ сэдвийн бодлогууд ЭЕШ -д орж ирдэг. Математик статистикийн бодлогуудыг бодоход үзүүлэлтүүдийг тооцох томьёонуудыг цээжээр мэдэхийн дээр тухайн үзүүлэлт юуг илэрхийлж байгааг сайн ойлгосон байх ёстой. Учир нь өгөгдлийг боловсруулах, үзүүлэлтүүдийг тооцох аргачлал тогтсон дүрмээр буюу томьёогоор хийгдэх тул алгебрийн бодлого шиг олон янзын аргаар бодох боломжгүйтэй холбоотой.
Математикийн теорем, томьёонуудыг сайн ойлгон тогтоохын зэрэгцээ онолын үндсэн ойлголт, ухагдхуунуудыг маш сайн мэдэж байх нь бодлого бодох үндэс болдог. Онолын ерөнхий мэдлэггүйгээр дан ганц томьёонуудаар бодлогыг шийдэх хэцүү. Ихэнх сурагчид томьёо мэдэж байхад бодлогыг бодно гэж буруу ойлгосон байх нь элбэг. Гэтэл хэзээ, хаана ямар томьёог хэрэглэх вэ? гэдэг нь онолын үндэслэлтэй байдаг нь математикийг хүнд мэт болгодог байх талтай. Бодлогын бодолтыг хараад ч ойлгохгүй үе бий. Энэ бол танд онолын ерөнхий мэдэгдхүүн дутаж байгаа хэлбэр. Үүнийг харгалзан үзээд математикийн ерөнхий онолын асуулт хэсгийг тусдаа бүлэг болгон орууллаа.





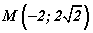 цэгээс координатийн эх хүртлэх зайг олоорой.
цэгээс координатийн эх хүртлэх зайг олоорой.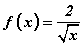 функцийн хувьд f'(4) -ийн утгыг олоорой.
функцийн хувьд f'(4) -ийн утгыг олоорой.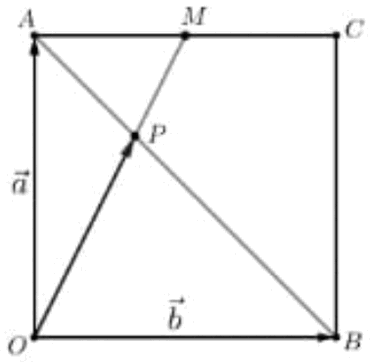 OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв
OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв 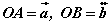 бол
бол 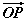 -ийг
-ийг 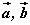 -ээр илэрхийл.
-ээр илэрхийл.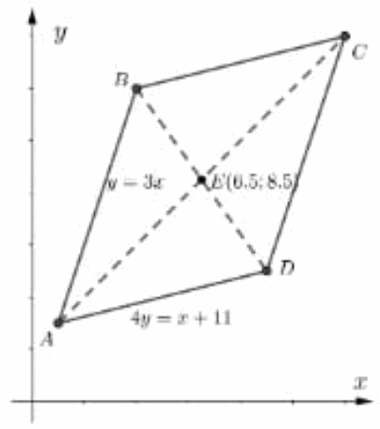 ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой.
ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой. AB диаметр ба
AB диаметр ба 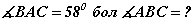 .
.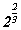 зэргийг язгуур хэрэглэн бичээрэй.
зэргийг язгуур хэрэглэн бичээрэй.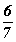 тооны урвуу тоог олоорой.
тооны урвуу тоог олоорой.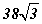 талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.
талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.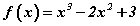 функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.
функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич. тэгшитгэлийг бод.
тэгшитгэлийг бод.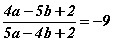 бол
бол 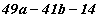 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.