Арифметик бол математикийн үндсэн суурь мэдлэгийг олгодог болохоор энэ сэдвийн бодлогыг заавал бодож сурсан байх хэрэгтэй. Математикийн энгийн үйлдлүүд байдаг болохоор хүүхдүүд их амархан мэтээр ойлгон нэг их тоохгүй байдгаас үүдэн алдаа хийх нь элбэг байдаг.
Ерөнхий шалгалтанд математикийн хичээлээр хүчээ сорих гэж буй хүүхэд багачуудад зориулан энэхүү хэсгийг нээж байгаа юм. Төгсөлтийн, ерөнхий, элсэлтийн шалгалтанд ирж байсан болон бодлого бодох ерөнхий зарчмуудыг ойлгоход тусламж болохоор төрөл бүрийн сэдвээр бодлогууд тавигдах болно.
Үсэг тоон илэрхийлэлд хувиргалт хийж сурах бол бодлого бодохын суурь болдог. Энэ сэдвийн бодлогын бодолтыг сайн эзэмшснээр цаашид ямарч төрлийн бодлогыг бодоход чухал нөлөө үзүүлдэг.
Үл мэдэгдэгч агуулсан энгийн тэгшитгэлүүдийг сайн ойлгож бодож сурснаар логарифм, илтгэгч, тригнометрийн тэгшитгэлүүдийг бодоход хөнгөн байх болно. Тэгшитгэл бодох нь үйлдлүүдийг гүйцэтгэх техник ажиллагааг алдаагүй зөв хийж сурах, томьёог тогтооход их чухал байдаг. Иймээс энэ хэсгийн бодлогуудаас шалгалт шүүлэгт тогтмол орж ирдэг юм шүү.
Вектор болон хуурмаг тоо тухай ойлголтууд ерөнхийдөө нилээд түвэгтэй асуудлыг үүсгэдэг. Хуурмаг тооны хувьд ерөнхий боловсролын сургуульд бараг үздэггүй гэхэд болно. Харин вектор тооцооллын бодлогууд элбэг байдаг. Вектор тооцоолол хийхдээ зургаар түүний геометр утгыг сайн ойлгох юм бол бодлого нь нэг их хүндрэлгүй бодогдоно.
Тэгшитгэл, алгебрын хувиргалтуудтай харьцуулбал тэнцэл биш арай хүндхэн. Сурагчид тэнцэл бишийг бодохдоо багагүй асуудалд ордог талтай. Тэнцэл бишийг ашиглахгүй бодлого гэж бараг үгүй. Функцын тодорхойлогдох муж, бутархай утгатай байх хэсгийг тодорхойлох гээд олон газар ашиглана. Тухайн бодлогоор өгөгдсөн илэрхийлэл, функц, тэгшитгэл аль нь ч бай эхлээд түүний утгатай байх мужийг тогтоох хэрэгтэй болдог. Иймд энэ төрлийн бодлогыг бодож сусан байх зайлшгүй шаардлагатай.
Дараалал прогресс сэдвээс бодлого ороогүй шалгалт гэж бараг байхгүй байдаг. Энэ сэдэв цаашлаад анализын эхлэл болох тул сайтар ойлгосон байх хэрэгтэй. Ухагдхуунаа сайн ойлгоод хэдэн чухал томьёонуудыг мэдэж байвал бодлогууд нэг их хүнд биш. Дарааллын талаарх мэдлэг нь зарим төрлийн бодлогыг бодоход нэн хэрэгтэй болдог. Жишээ нь ердийн илэрхийллүүд дараалал байдлаар өгөгдсөн бодлогууд ихээр байдаг ч түүнийг бодлогын нөхцөлд дараалал гэдгийг заагаагүй байх гэх мэтээр
Геометрийн бодлогууд. Сурагчид энэ төрлийн бодлогоос нилээд айдаг. Энд томьёоноос гадна геометрийн дүрсүүдийн шинж чанар, теоремуудыг мэдэх шаардлага гарч ирдэг. Эдгээрийг мэдэж байхад бодлогууд тийм ч хүнд санагдахгүй.
Логарифм болон илтгэгч тэгшитгэлүүдийн бодлогууд. Энэ төрлийн бодлогууд шалгалт шүүлгийн үед ихээр орж ирдэг тул эдгээрийг бодож сурах хэрэгтэй. Үндсэн аргыг ойлгосон байхад бодох аргачлал нь ердийн тэгшитгэл бодохтой ижилхэн байдаг.
Комбинаторик. Ньютоны биномын төрлийн бодлогууд. Сэлгэмэл, гүйлэгмэл зэргийг сайн ойлгох нь цаашдаа магадлалын бодлого бодох үндэс болдог тул нилээд чухал сэдэвт орно. Ийм төрлийн бодлогууд таниас хийсвэр сэтгэлгээг шаардана.
Ерөнхий боловсролын сургуулийн хэмжээнд цэвэр огторгуйн геометрийн бодлогууд ордоггүй. Зөвхөн хавтгайн гурван хэмжээст орон зайн бодлогууд байдаг. Ийм төрлийн бодлогыг бодохдоо зургийг маш сайн ойлгон зурж сурах нь хамгийн чухал. Зураглалыг сайн гаргаж чадвал бодлогыг бодоход амархан болдог.





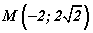 цэгээс координатийн эх хүртлэх зайг олоорой.
цэгээс координатийн эх хүртлэх зайг олоорой.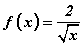 функцийн хувьд f'(4) -ийн утгыг олоорой.
функцийн хувьд f'(4) -ийн утгыг олоорой.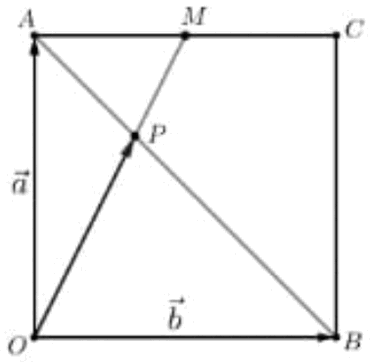 OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв
OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв 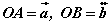 бол
бол 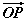 -ийг
-ийг 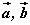 -ээр илэрхийл.
-ээр илэрхийл.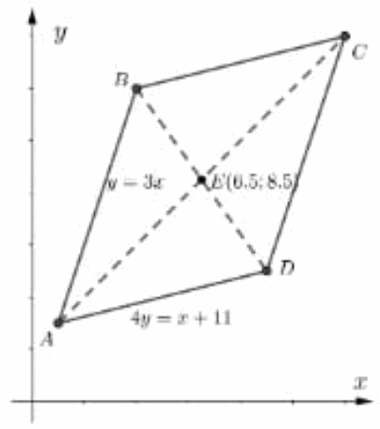 ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой.
ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой. AB диаметр ба
AB диаметр ба 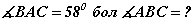 .
.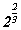 зэргийг язгуур хэрэглэн бичээрэй.
зэргийг язгуур хэрэглэн бичээрэй.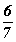 тооны урвуу тоог олоорой.
тооны урвуу тоог олоорой.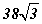 талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.
талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.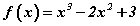 функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.
функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич. тэгшитгэлийг бод.
тэгшитгэлийг бод.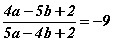 бол
бол 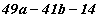 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.