1.c4 e5 2.Мc3 Мf6 3.Мf3 Мc6 4.e3 Тe7 5.d4 exd4 6.Мxd4 O-O 7.Тe2 d5 8.Мxc6 bxc6 9.O-O Тd6 10.b3 Бe7 11.Тb2 гэж цагаан арай илүү хүүний бүтэцтэй Англи гарааны онолын хувилбарыг тоглосон. Харин харын боднууд идэвхитэй байрласан. Тэдэнд цагаан d5 нүдэнд үзүүлэх дарамтыг сааруулах боломжууд бий. d5 нүдний хамгаалалтын асуудлыг илүү шийдэх аргыг сонгоно уу.
- 11... Тe6 гаар төвийг бэхжүүлэх
- 11... Трd8 гэж төвийн хүүгээ шууд бусаар хамгаалах
- Хүүний бүтцээ эвдэн 11... dxc4 гэж хүүг аван боднуудын идэвхитэй тоглолтыг авах.
Зөвлөмж: Мастеруудын өрөг тул үргэлжлэлийн хувилбар бүрд нилээд шинжилгээ хэрэгтэй. Бодлогод тавигдсан хувилбараас өөр нүүдлийг ч олж болох талтай. Эхний үед зөв үргэлжлэлийг сайн олохгүй байж болох ч шатарт суралцах сайн дадлага гэдэгт эргэлзэх зүйлгүй.





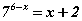 тэгшитгэлийг бод.
тэгшитгэлийг бод.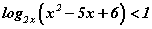 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.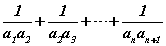 нийлбэрийг ол.
нийлбэрийг ол.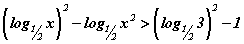 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.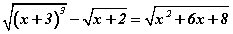 тэгшитгэлийн шийд
тэгшитгэлийн шийд 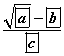 .
.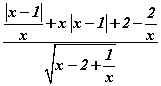 илэрхийлэл
илэрхийлэл 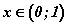 интервалд
интервалд 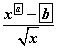 ,
, 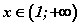 интервалд
интервалд 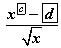 байна.
байна.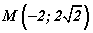 цэгээс координатийн эх хүртлэх зайг олоорой.
цэгээс координатийн эх хүртлэх зайг олоорой.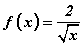 функцийн хувьд f'(4) -ийн утгыг олоорой.
функцийн хувьд f'(4) -ийн утгыг олоорой.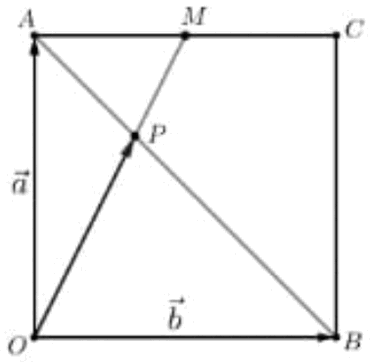 OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв
OACB квадратийн AC талын дундаж цэг M ба AB диагональ OM хэрчимтэй P цэгт огтлолцдог. Хэрэв 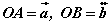 бол
бол 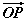 -ийг
-ийг 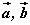 -ээр илэрхийл.
-ээр илэрхийл.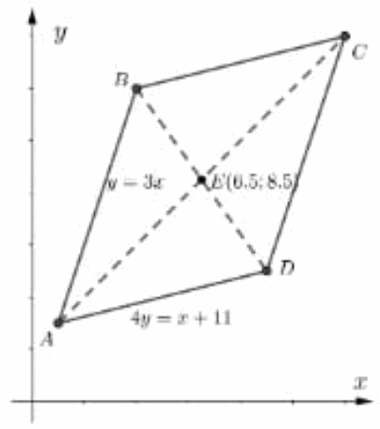 ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой.
ABCD параллелограммийн AB тал y=3x тэгшитгэлтэй, AD тал 4y=x+11 тэгшитгэлтэй. AC ба BD диагоналиуд нь E(6,5; 8,5) цэгт огтлолцдог бол C цэгийн координатийг олоорой. AB диаметр ба
AB диаметр ба 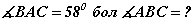 .
.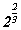 зэргийг язгуур хэрэглэн бичээрэй.
зэргийг язгуур хэрэглэн бичээрэй.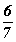 тооны урвуу тоог олоорой.
тооны урвуу тоог олоорой.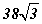 талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.
талтай зөв гурвалжнд багтсан тойргийн радиусыг ол.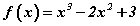 функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.
функцийн графикийн x=1 цэгт татсан шүргэгчийн тэгшитгэлийг бич.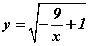 функцийн тодорхойлогдох мужийг ол.
функцийн тодорхойлогдох мужийг ол.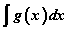 -ийг ол.
-ийг ол.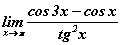 хязгаарыг ол.
хязгаарыг ол.