Дөрвөн сандалд 4 хүн хэдэн аргаар суух боломжтой вэ? Нэг сандалд нэг хүн л сууна.
Комбинаторик. Магадлал ( 140 )
Комбинаторик. Ньютоны биномын төрлийн бодлогууд. Сэлгэмэл, гүйлэгмэл зэргийг сайн ойлгох нь цаашдаа магадлалын бодлого бодох үндэс болдог тул нилээд чухал сэдэвт орно. Ийм төрлийн бодлогууд таниас хийсвэр сэтгэлгээг шаардана.
Нээгдсэн тоо: 1298 Бүртгүүлэх
Сейфний түлхүүр 6 цифрээс бүрдэнэ. Түлхүүрийн цифрүүдийг дараалуулан оруулахаас гадна түлхүүрт цифрүүд давхардаж болно. Тэгвэл түлхүүр зохиох боломжит хувилбарын тоо хэд байх вэ?
Нээгдсэн тоо: 1930 Нийтийн
Өдрийн хуваарьт 5 хичээл ордог. Тэгвэл 11 хичээлээс зохиож болох хуваарийн хувилбарын тоог ол. Нэг хичээл өдөрт нэг удаа л орно.
Нээгдсэн тоо: 1814 Нийтийн
Шуудангийн салбарт 10 төрлийн мэндчилгээ зарагдаж байв. 12 мэндчилгээг хэдэн аргаар худалдан авч болох вэ?
Нээгдсэн тоо: 2504 Нийтийн
Агуулахад 10 хайрцаг байв. Хэрвээ нэг машин 5 хайрцагийг авч явах даацтай бол хайрцагуудыг 2 машин хэдэн янзаар авч явах боломжтой вэ?
Нээгдсэн тоо: 1715 Бүртгүүлэх
Хайрцагт байгаа 1-р төрлийн 5 ширхэг, 2-р төрлийн 7 ширхэг алимнаас таамгаар 2 ширхэгийг сонгон авахад тэдгээр нь өөр өөр төрлийн алим байх үзэгдлийн магадлалыг ол.
Нээгдсэн тоо: 1376 Төлбөртэй
Хайрцагт 12 өнгийн будаг байв. Санамсаргүйгээр 3-ыг сонгон авч тус бүрээр нь нэг нэг дугуй зурсан ба тэдгээрийгээ буцааж хийгээд дахин санамсаргүйгээр 3-ыг сонгон авч тус бүрээр нь нэг нэг дөрвөлжин зурав. Цаасан дээр хэдэн ялгаатай дүрслэл үүсэх боломжтой вэ? (Дүрс нь хэлбэр эсвэл өнгөөрөө ялгаатай бол ялгаатайд тооцно)
Нээгдсэн тоо: 1667 Төлбөртэй
Бүх талст нь будагтай кубыг 1000 ширхэг тэнцүү хэсэгт хуваав. Эдгээр кубүүдээс таамгаар 1-г сонгоход ядаж 2 талс нь будагтай куб таарах магадлалыг ол.
Нээгдсэн тоо: 1226 Төлбөртэй
1, 2, 3, 4, 5, 6 цифрүүдийг ашиглан цифр давталгүй, 2 ба 4 цифр зэрэгцэн орсон байх таван оронтой хичнээн тоо үүсгэж болох вэ?
Нээгдсэн тоо: 1189 Төлбөртэй
9 ширхэг том, 12 ширхэг жижиг хайрцаг байв. Том хайрцаг бүрт 8 улаан, 6 хөх; жижиг хайрцаг бүрт 10 улаан, 6 хөх бөмбөг байв. Таамгаар нэг хайрцаг авч түүнээс нэг бөмбөг авъя.
- Авсан хайрцаг том байх магадлал
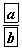
- Авсан бөмбөг том хайрцагны улаан байх магадлал
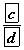
- Хайрцаг том бөгөөд бөмбөг улаан байх магадлал
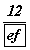
- Бөмбөг улаан байх магадлал
Энэ долоо хоногт
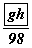
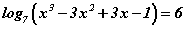тэгшитгэлийг бод.