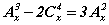тэгшитгэлийг бод.
Комбинаторик. Магадлал ( 140 )
Комбинаторик. Ньютоны биномын төрлийн бодлогууд. Сэлгэмэл, гүйлэгмэл зэргийг сайн ойлгох нь цаашдаа магадлалын бодлого бодох үндэс болдог тул нилээд чухал сэдэвт орно. Ийм төрлийн бодлогууд таниас хийсвэр сэтгэлгээг шаардана.
тэгшитгэлийг бод.Нээгдсэн тоо: 1319 Төлбөртэй
2 оронтой тоонуудаас таамгаар нэг тоо сонгоход сонгогдсон тоо:
- 1 -ийн цифр агуулсан байх магадлал
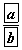
- 1 ба 2 цифрийн дор хаяж нэгийг агуулсан байх магадлал
- 3 -д хуваагддаг байх магадлал
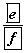
- 1 -ийн цифр агуулсан ба 3 -д хуваагддаг байх магадлал
Нээгдсэн тоо: 1642 Төлбөртэй
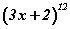биномын задаргааны x5 -ийн өмнөх коэффициентийг ол.
Нээгдсэн тоо: 1272 Төлбөртэй
Хайрцагт 5 улаан, 3 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
Нээгдсэн тоо: 1378 Төлбөртэй
Нэгж радиустай дугуй дотроос таамгаар нэг цэг авахад дугуйн төвөөс 1/3 -ээс бага зайд байх магадлалыг ол.
Нээгдсэн тоо: 2095 Нийтийн
Дэлгүүрт бие биеэсээ үл хамаарах хоёр автомат машин ажиллах ба тэдгээрийн аль нэг нь ажиллахгүй болох магадлал 0,05 бол дор хаяад нэг машин ажиллаж байх магадлалыг ол.
Нээгдсэн тоо: 1739 Төлбөртэй
Биатлончин байнд таван удаа буудна. Нэг удаагийн буудалтаар түүний байгаа онох магадлал 0,8 бол тэр эхний гурван буудалтаар байгаа оноод харин сүүлийн хоёрт онохгүй байх магадлалыг ол. Үр дүнг зууны нарийвчлалаар гарга.
Нээгдсэн тоо: 1614 Нийтийн
Шатарчин А цагаанаар тогловол шатарчин Б -г хожих магадлал 0,52. Хэрвээ А хараар тогловол Б -г хожих магадлал 0,3. Шатарчид хоёр өрөг тоглох бөгөөд хоёрдугаар өрөгт өнгөө солин тоглоно. А шатарчин хоёр өрөгт хоёуланд нь хожих магадлалыг ол. Шатарчид тэнцэхгүй гэж үзнэ.
Нээгдсэн тоо: 1914 Нийтийн
Ижил загварын сав хийдэг хоёр үйлдвэр байжээ. Нэгдүгээр үйлдвэр нийт савны 45% -ийг харин хоёрдугаар үйлдвэр 55% -ийг нийлүүлдэг. Нэгдүгээр үйлдвэрийн савнуудын 3% гэмтэлтэй харин хоёрдугаар үйлдвэрийнх 1% гэмтэлтэй гардаг бол санамсаргүйгээр дэлгүүрээс авсан сав гэмтэлтэй байх магадлалыг ол.
Энэ долоо хоногт
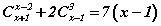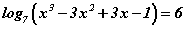тэгшитгэлийг бод.