Порпорц
Порпорц гэдэг нь хоёр харьцааны тэнцэл юм.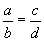 порпорцоос ad=bc / диагнолд байрлах гишүүдийн үржвэр тэнцүү / гарна. Мөн түүнчлэн ad=bc тэнцлээс дараах порпорцууд гарна.
порпорцоос ad=bc / диагнолд байрлах гишүүдийн үржвэр тэнцүү / гарна. Мөн түүнчлэн ad=bc тэнцлээс дараах порпорцууд гарна.
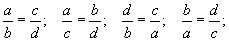
Эдгээр болон бусад порпорцыг анхны 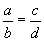 порпорцоос дараах дүрмээр гарган авна.
порпорцоос дараах дүрмээр гарган авна.
- Порпорцын диагнолд байрлах гишүүдийн байрыг сольж болно.
- Порпорцийн харьцааг эсрэгээр сольж болно.
Үүсмэл порпорц.
Хэрвээ 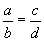 бол анхны порпорцоос гарсан дараах үүсмэл порпорцууд байж болно.
бол анхны порпорцоос гарсан дараах үүсмэл порпорцууд байж болно.
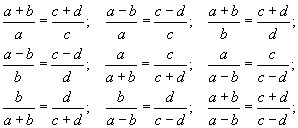
Эдгээр болон бусад порпорцыг үндсэн хоёр томьёогоор нэгтгэж болно.
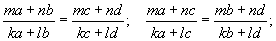
Энд m, n, k, l нь дурын тоонууд.
Жишээ
Хэрвээ m = n = k =1, l=0 бол 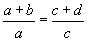 гарна.
гарна.





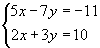 тэгшитгэлийн системийг бод.
тэгшитгэлийн системийг бод. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.