Тригнометрийн тэгшитгэлүүдийг бодох томьёонууд.
төрлийн тэгшитгэлүүдийг тригнометрийн энгийн тэгшитгэл гэдэг. Эдгээр тэгшитгэлүүдийг бодох томьёонууд :
Тайлбар : n - бүхэл тоо,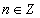 
| Дугаар | Томьёо |
| 8.1.1 |  |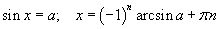
| 8.1.2 |  |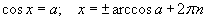
| 8.1.3 |  |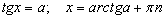
| 8.1.4 |  |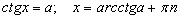
a=0, a=1, a=-1 байх тухайн тохиолдлуудад дараах томьёонууд хүчинтэй.
| Дугаар | Томьёо |
| 8.2.1 |  |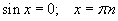
| 8.2.2 |  |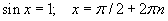
| 8.2.3 |  |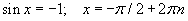
| 8.2.4 |  |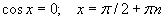
| 8.2.5 |  |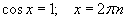
| 8.2.6 |  |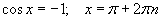
| 8.2.7 |  |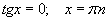
| 8.2.8 |  |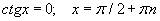
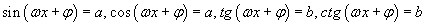энд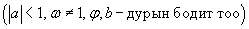 
төрлийн тэгшитгэлүүд нь тригнометрийн энгийн тэгшитгэлүүдэд бас хамаарагдана. Эдгээрийг бодоходоо 
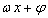г x ээр орлуулаад 8.1.1-8.1.4 томьёонуудыг хэрэглэнэ.
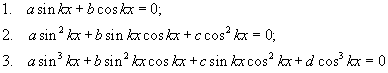
1, 2, 3 эдгээрийг тригнометрийн түгээмэл хэв шинжит тэгшитгэлүүд гэдэг.
d≠0 үед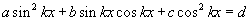 
нь түгээмэл хэв шинжит тэгшитгэлд орохгүй. Гэхдээ ийм тэгшитгэлийг d тоог 
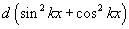гэсэн ижил тэнцлээр сольж 2-р хэлбэрийн тэгшитгэлд хувиргаж болдог.
- a≠0 байхад 1, 2, 3 тэгшитгэлүүдийг бодохдоо coskx=0 байлгах x ийн утгыг авч үзнэ. Тэгвэл x ийн coskx=0 байлгах утганд sinkx=0 байх ёстой гэдэг нь тэгшитгэл бүрээс гарах бөгөөд энэ нь боломжгүй юм. Тэгэхлээр эдгээр тэгшитгэлүүд нь зөвхөн coskx≠0 байлгах x ийн утганд бодолттой байна. Иймээс a≠0 байхад тэгшитгэлүүдийн хоёр талыг 1.-г cosx -д, 2.-г cos2x -д, 3.-г cos3x -д хуваавал шийдийн алдагдал гарахгүй. Хуваалтын үр дүнд tgkx тэй алгебрын тэгшитгэл гарах бөгөөд tgkx=z орлуулга хийх замаар бодно.
- a=0 байхад coskx=0 байлгах x ийн утгыг алдагдахад хүргэх учраас 1, 2, 3 тэгшитгэлүүдийг coskx д хувааж болохгүй. a=0 байхад 1 тэгшитгэл нь энгийн тэгшитгэл болно. Харин 2, 3-р тэгшитгэлүүдийг үржигдхүүнд задалж боддог.
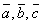- векторууд, 
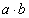- векторуудын скаляр үржвэр, |a| - векторын урт
функцийн тодорхойлогдох мужийг ол.
-ийг ол.
хязгаарыг ол.