Гурвалжин, дөрвөн өнцөгт, олон өнцөгт, тойрог, дугуй, секторийн хэмжээсүүдийг олох томьёонууд
Дурын гурвалжин
(a, b, c - талууд, α, β, γ - талуудын эсрэг орших өнцгүүд, p - хагас периметр, R - багтаасан тойргийн радиус, r - багтсан тойргийн радиус, S - талбай, ha- a - талд буулгасан өндөр)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.1.1 |
Нэг тал өндрөөр |
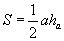 |
| 15.1.2 |
Хоёр тал тэдгээрийн хоорондох өнцгөөр |
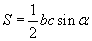 |
| 15.1.3 |
Героны томьёо |
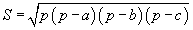 |
| 15.1.4 |
Багтсан тойргийн радиус |
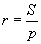 |
| 15.1.5 |
Багтаасан тойргийн радиус |
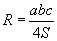 |
| 15.1.6 |
Нэг тал гурван өнцгөөр |
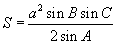 |
| 15.1.7 |
Косинусын теорем |
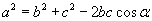 |
| 15.1.8 |
Синусын теорем |
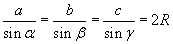 |
Тэгш өнцөгт гурвалжин
(a, b - катетууд, c - гипотенуз, ac, bc- гипотенуз дээрх катетуудын проекц)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.2.1 |
Катетуудаар талбайг олох |
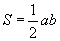 |
| 15.2.2 |
Гипотенуз ба түүнд буулгасан өндрөөр |
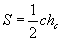 |
| 15.2.3 |
Багтсан тойргийн радиус |
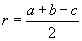 |
| 15.2.4 |
Багтаасан тойргийн радиус |
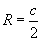 |
| 15.2.5 |
Пифагорын теорем |
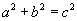 |
| 15.2.6 |
Катетууд ба гипотенузэд буулгасан өндрийн харьцаа |
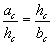 |
| 15.2.7 |
Катет гипотенузын харьцаа |
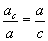 |
| 15.2.8 |
Катет гипотенузын харьцаа |
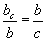 |
| 15.2.9 |
Катетыг олох |
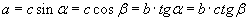 |
Адил хажуут гурвалжин
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.3.1 |
Талбай |
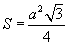 |
| 15.3.2 |
Багтсан тойргийн радиус |
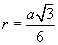 |
| 15.3.3 |
Багтаасан тойргийн радиус |
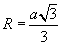 |
Гүдгэр дөрвөн өнцөгт
(d1 , d2 - диагналууд, 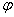 - диагнал хоорондын өнцөг, a, b - хамар талууд, α - хамар талуудын хоорондын өнцөг, ha- a- талд буулгасан өндөр S - талбай)
- диагнал хоорондын өнцөг, a, b - хамар талууд, α - хамар талуудын хоорондын өнцөг, ha- a- талд буулгасан өндөр S - талбай)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.1 |
Дурын дөрвөн өнцөгт |
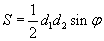 |
| 15.4.2 |
Паралелграм |
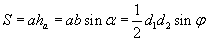 |
| 15.4.3 |
Ромб |
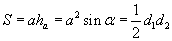 |
| 15.4.4 |
Тэгш өнцөгт |
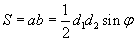 |
| 15.4.5 |
Квадрат |
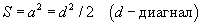 |
Трапец
(a, b - сууриуд, h - суурь хоорондын зай, l - дундаж шугам)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.6 |
Трапецын дундаж шугам |
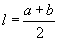 |
| 15.4.7 |
Трапецын талбай |
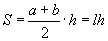 |
Багтаасан олон өнцөгт
(p - хагас периметр, r - багтсан тойргийн радиус)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.8 |
Олон өнцөгтийн талбай |
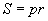 |
Зөв олон өнцөгт
(an - зөв n өнцөгтийн тал, R - багтаасан тойргийн радиус, r - багтсан тойргийн радиус)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.9 |
Талууд |
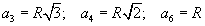 |
| 15.4.10 |
Талбай |
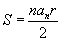 |
Тойрог
(r - радиус, C - тойргийн урт, S - дугуйн талбай)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.11 |
Тойргийн урт |
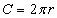 |
| 15.4.12 |
Дугуйн талбай |
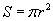 |
Сектор
(l - сектороор хязгаарлагдсан нумын урт, n0 - төв өнцгийн градус хэмжээ, α - төв өнцгийн радиан хэмжээ)
| Дугаар |
Тодорхойлолт |
Томьёо |
| 15.4.13 |
Нумын урт |
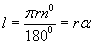 |
| 15.4.14 |
Секторын талбай |
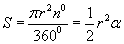 |
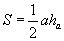
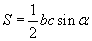
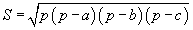
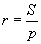
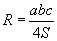
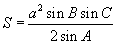
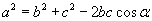
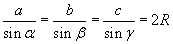
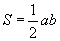
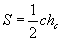
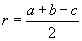
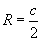
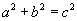
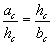
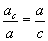
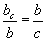
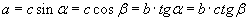





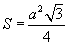
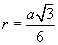
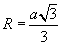
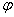 - диагнал хоорондын өнцөг, a, b - хамар талууд, α - хамар талуудын хоорондын өнцөг, ha- a- талд буулгасан өндөр S - талбай)
- диагнал хоорондын өнцөг, a, b - хамар талууд, α - хамар талуудын хоорондын өнцөг, ha- a- талд буулгасан өндөр S - талбай)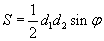
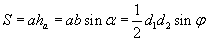
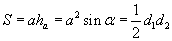
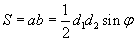
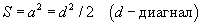
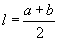
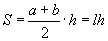
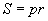
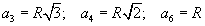
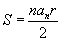
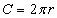
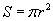
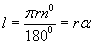
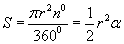
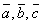 - векторууд,
- векторууд, 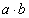 - векторуудын скаляр үржвэр, |a| - векторын урт
- векторуудын скаляр үржвэр, |a| - векторын урт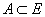 - A нь E олонлогт харьяалагдана,
- A нь E олонлогт харьяалагдана, 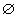 - хоосон олонлог, P(A) - A үзэгдэлийн магадлал
- хоосон олонлог, P(A) - A үзэгдэлийн магадлал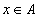 - x нь A олонлогт харьяалагдана,
- x нь A олонлогт харьяалагдана, 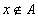 - x нь A олонлогт харьяалагдахгүй,
- x нь A олонлогт харьяалагдахгүй, 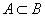 - A олонлог B олонлогт багтана,
- A олонлог B олонлогт багтана, 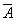 - олонлогийн гүйцээлт.
- олонлогийн гүйцээлт. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.