Математикийн бодлого бодох яагаад хүнд байдаг вэ? гэвэл энд бүх зүйлийг ямар нэгэн алдаа гаргахгүй хийх хэрэгтэй болдог. Алдаа гаргавал тэр дороо алдаа гэж мэдэгдэхгүй та зүгээр л өөр бодлого бодох ажиллагаанд шилжээд явдаг. Тэгвэл бодлого биш жишээ нь гадаад хэл, уран зохиол, нийгмийн чиглэлийн асуудлыг буруу зөрүү явсан байсан ч зөв замдаа шууд ороод шийдэх боломжтой. Харин бодлого бодоход ийм зүйл байхгүй. Алдаа л хийсэн бол буруу зам руу орно. Үүнийгээ мэдэхгүй бол алдаа болно мэдвэл бараг эхнээс нь шалгах хэрэгтэй болно.

Иймд үйлдлүүдийг хийх ажиллагааг сайн эзэмшсэн байвал зохино. Математикийн нэмэх, хасах, хуваах, үржих үндсэн үйлдлүүдийг сурагчид сайн эзэмшсэн байдаг боловч эдгээр үйлдлүүдийг бутархай дээр ялангуяа хураах ажиллагаанд ашиглахдаа алдааг ихээр гаргадаг. Энэ хичээлээр бид бутархайг хураахдаа гаргадаг алдаануудыг жишээн дээр авч үзэцгээе.

Бодлого.
Гөлөг өдөрт 200 грамм хоол иддэг байжээ. 14 хоногийн дараа тэр өссөн тул өдөрт 20% илүү хоол идэх болжээ. Одоо гөлөг хичнээн грамм хоол иддэг болсон бэ?

Буруу бодолт. Хувь тооцох энэхүү бодлого нь 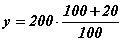гэсэн тэгшитгэлийг бодоход шилжинэ. Их олон сурагчид бутархайн хүртвэр болон хуваарт байгаа 100-г хураан 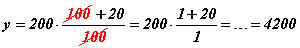гэж бодон алдаа хийдэг. Гарсан хариулт мэдээж буруу. 200 грамм хоол идэж байсан гөлөг 4200 граммыг иддэг болсон гэдэг нь 20 хувиар биш 21 дахин их болсон гэсэн үг. Бутархайн хүртвэр хуваарт ижилхэн тоо, илэрхийлэл харагдах л юм бол хураах гээд байж болохгүй. Ийм алдаанд орохгүйн тулд доорх дүрмийг цээжлэн тогтоож аваарай.

Үржигдхүүнүүдийг л зөвхөн хурааж болно. Ялгавар, нийлбэртэй бол хурааж болохгүй.  

Дээрх бодлогын зөв бодолт 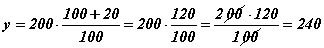байх болно. Бутархайн хүртвэр хуваарт зөвхөн үржигдхүүнүүд л байгаа тул хураах бүрэн боломжтой. Ямар ч нэмэх, хасах тэмгүүд байхгүй.

Дахин нэг жишээ авъя.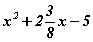
илэрхийллийг хялбарчил. Энд 2 ба 8 -ыг шууд 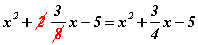гэж хураан алдаа ихээр гаргадаг. Ингээд эхэлсэн бол цаашаа мэдээж буруу хариу гаргана. Энд бидний дассан зүйл алдаа гаргах үндэс болдог. Илэрхийлэлд үржүүлэхийн тэмдгийг шаардлагагүй тохиолдолд бичдэггүй. Жишээ 2x, 15xy гэх мэтээр. Гэтэл дээрх дүрмийг сайн мэддэг сурагчид хүртэл энд үржих тэмдэг байгаа гэж үзээд шууд хурааж орхидог. Гэтэл энд үржих тэмдэг биш нэмэх тэмдэг байгаа. Бутархайн бичилт нэгэнт ийм хойно бид өөрсдөө л үүнийг ойлгох хэрэгтэй. Харахад хураахад буруу зүйлгүй мэт. Гэвч энэ бичлэгийг ойлгохдоо 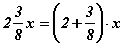гэж харах ёстой. Аравтын бутархайн хувьд бүхэл хэсэг бутархай хэсгийг таслалаар заагласан байдаг тул амар. Харин энгийн бутархайн бичлэгийн энэ хэлбэрийг зөв ойлгох хэрэгтэй. Хэрвээ илэрхийлэлд 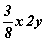гэж өгөгдсөн бол хураахад буруу болохгүй. Учир нь энд бүгд үржигдхүүнүүд байгаа биз дээ.

Асуудал үүсгэдэг бас зүйл бол порпорц байдаг. Ялангуяа хувьсагч хоёр талдаа байрласан үе.

Жишээ нь 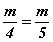тэгшитгэлийг бод.
Буруу бодолт. Зарим сурагчид тэгшитгэлийн хоёр талыг m -д хураан хэзээ ч тэнцэхгүй 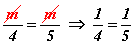илэрхийлэл гарган ирдэг.
Зөв бодолт. Энэ бол ердийн шугаман тэгшитгэл. Тэгшитгэлийн бүх гишүүдийг тэнцүүгийн тэмдэгийн нэг талд гараад эсхүл порпорцийн чанарыг ашиглаад бодсон ч болно.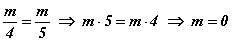
Та эхний бодолтонд ямар алдаа байгаа юм гэж асууж болно. Үүнийг тайлбарлахын тулд тэгшитгэлтэй ажиллах

Ямарч тэгшитгэлийг тэгээс ялгаатай дурын тоонд үржүүлж хувааж болно.

дүрмийг саная. Хэрэгтэй дүрэм тул тогтоон аварай. Зөвхөн тэгээс ялгаатай тоонд л хувааж болно. Манай тохиолдолд зөвхөн m≠0 үед л тэгшитгэлийг m -д хувааж болно. Хэрвээ m=0 бол яах вэ? Утгыг тэгшитгэлд тавиад шалгавал 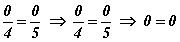зөв тэнцэл гарах тул m=0 бол шийд. Харин m≠0 бусад тохиолдолд 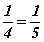гэсэн буруу илэрхийлэл гарна.

Дээрх алдаануудаас дүгнэвэл

1. Үржигдхүүнүүдийг л зөвхөн хураана. Нийлбэр, ялгаварыг болохгүй. Иймээс хүртвэр, хуваарийг үржигдхүүнд задлаж сурах хэрэгтэй.
2. Порпорцийн захын гишүүдийн үржвэр дундах гишүүдийн үржвэртэй тэнцүү. Порпорцийн үндсэн чанар
3. Тэгшитгэлийг зөвхөн тэгээс ялгаатай k тоогоор үржүүлж эсхүл хувааж болно. k=0 тохиолдолыг тусд нь шалгах хэрэгтэй.

гэсэн гурван дүрмийг тогтоон аваарай.