12,15,18 см талуудтай гурвалжин өгөгджээ. Их тал дээр төвтэй нөгөө хоёр талыг нь шүргэсэн тойрог татахад их тал тойргийн төвөөр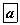 
болон 
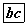урттай хэрчимд хуваагдах бол a, b, c -гийн утгыг ол.
Хавтгайн геометр ( 166 )
Геометрийн бодлогууд. Сурагчид энэ төрлийн бодлогоос нилээд айдаг. Энд томьёоноос гадна геометрийн дүрсүүдийн шинж чанар, теоремуудыг мэдэх шаардлага гарч ирдэг. Эдгээрийг мэдэж байхад бодлогууд тийм ч хүнд санагдахгүй.
Нээгдсэн тоо: 1314 Төлбөртэй
Нээгдсэн тоо: 1594 Төлбөртэй
Адил хажуут гурвалжны суурь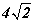 
см, харин хажуу талд татсан медиан 5 см бол гурвалжны хажуу талыг ол.
Нээгдсэн тоо: 1689 Төлбөртэй
Зөв гурвалжны суурь, талууд ижил гурван хэсэгт хуваагдсан ба хуваалтын харгалзах цэгүүдийг нэг чиглэлд хооронд нь холбосон. Үүссэн зөв гурвалжинд 6 см радиустай тойрог багтсан бол том гурвалжны тал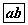 
байна.
Нээгдсэн тоо: 1547 Төлбөртэй
Адил хажуут гурвалжны суурь 16 см, харин талууд нь 10 см бол гурвалжинд багтсан болон багтаасан тойргийн төвүүдийн хоорондын зайг ол.
Нээгдсэн тоо: 1390 Төлбөртэй
4 см талтай адил хажуут гурвалжны хажуу талд медиан татсан. Хэрвээ медиан нь 3 см бол гурвалжны суурийг ол.
Нээгдсэн тоо: 1850 Төлбөртэй
17 см талтай адил хажуут трапецэд 15 см диаметртэй тойрог багтсан бол трапецын сууриудын уртыг ол.
Нээгдсэн тоо: 1101 Төлбөртэй
a ба b катеттай тэгш өнцөгт гурвалжин ерөнхий тэгш өнцөгтэй квадратыг багтаасан бол квадратын периметрийг ол.
Нээгдсэн тоо: 1651 Төлбөртэй
Ромбын мохоо өнцгөөс татсан өндөр түүний талыг m ба n урттай хэрчимд хуваах бол ромбын диагналуудыг ол.
Нээгдсэн тоо: 1653 Төлбөртэй
Адил хажуут трапецын сууриуд 21 ба 9 см. Трапецын өндөр 8 см бол трапецыг багтаасан тойргийн радиусыг ол.
Нээгдсэн тоо: 1273 Төлбөртэй
Адил хажуут трапецын сууриуд 20 ба 12 см. Трапецыг багтаасан тойргийн төв их суурь дээр байрлах бол трапецын диагналыг ол.
Энэ долоо хоногт
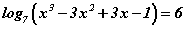тэгшитгэлийг бод.