Ямарч натурал тоог ангилалын бүрдүүлэгчдийн нийлбэр хэлбэрээр илэрхийлж болно.
Үүнийг ойлгохын тулд 999 тоог аваад үзье. 999 тоо нь 9 зуут, 9 аравт, 9 нэгжээс бүрдэнэ.
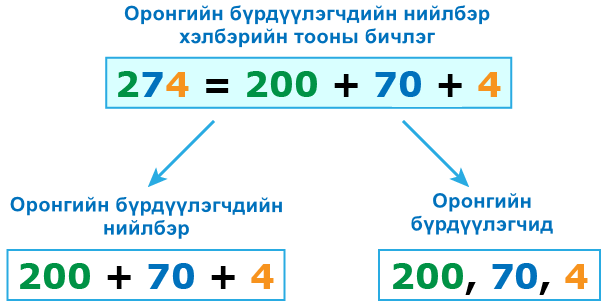
Тэгвэл 999 = 9 зуут + 9 аравт + 9 нэгж = 900 + 90 + 9 гэсэн үг.
Дээрх бичлэгийн 900, 90, 9 бол оронгийн бүрдүүлэгчид.
Оронгийн бүрдүүлэгч гэдэг нь тухайн орон дахь нэгжийн тоо.
Оронгийн бүрдүүлэгчдийн нийлбэрийг 999 = 9 · 100 + 9 · 10 + 9 · 1 гэж бичиж болно.
Оронгийн бүрдүүлэгчийг үржүүлж буй (1, 10, 100, 1000 г.м) тоог оронгийн нэгж гэнэ.
Жишээ нь 1 - нэгжийн оронгийн нэгж, 10 - аравтын оронгийн нэгж, 100 - зуутын оронгийн нэгж гэх мэтээр.
Оронгийн нэгжээр үржүүлэгдэж буй тоог оронгийн нэгжийн тоо гэнэ.
Ямарч тооны 12 = 1 · 10 + 2 · 1 эсхүл 12 = 10 + 2 хэлбэрийн бичлэгийг тооны оронгийн бүрдүүлэгчдийн задаргаа эсхүл оронгийн бүрдүүлэгчдийн нийлбэр гэж нэрлэнэ.
Оронгийн бүрдүүлэгчдийн нийлбэр гэдэг нь олон оронтой тоог түүний оронгийн нэгжийн нийлбэр хэлбэрээр илэрхийлсэн бичлэг.
Жишээ
4587, 4056, 2500 тоонудыг оронгийн бүрдүүлэгчдийн нийлбэрээр бич.
Бодолт
4587 = 4 · 1000 + 5 · 100 + 8 · 10 + 7 · 1 = 4000 + 500 + 80 + 7;
4056 = 4 · 1000 + 0 · 100 + 5 · 10 + 6 · 1 = 4000 + 50 + 6;
2500 = 2 · 1000 + 5 · 100 + 0 · 10 + 0 · 1 = 2000 + 500.
Оронгийн бүрдүүлэгчдийн нийлбэрээр тоог задлан бичих тун амархан. Та зөвхөн тооны ангилал буюу хэд дэх орон ямар ангилалын ямар нэгжээр илэрхийлэгдэхийг мэдэж байхад хангалттай. Жишээ 4587 тооны хувьд 4 мянгат, 5 зуут, 8 аравт, 7 нэгж гэдгээс л нийлбэр үүсч байгаа юм.
Тоог бүрдүүлэгчдийн нийлбэрээр задлан бичихэд 1000, 100, 10 гэх мэтээр олон тэгийг бичихэд төвөгтэй байвал түүнийг 10 -ын зэргээр
4587 = 4 · 103 + 5 · 102 + 8 · 101 + 7 · 1 = 4000 + 500 + 80 + 7;
4056 = 4 · 103 + 0 · 102 + 5 · 101 + 6 · 1 = 4000 + 50 + 6;
2500 = 2 · 103 + 5 · 102 + 0 · 101 + 0 · 1 = 2000 + 500.
орлуулан бичиж болно.





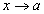 үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд
үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд 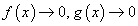 эсвэл,
эсвэл, 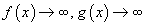 эсвэл
эсвэл 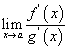 хязгаар байна.
хязгаар байна.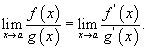 байна.
байна.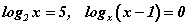
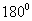 тэнцүү. KM шулуунтай перпендикуляр AB, CD, EF /Зур. 12/ шулуунууд нь өөр хоорондоо паралель байна. Паралель хоёр шулуунтай перпендикуляр шулууны урт нь паралель шулуунуудын хоорондын зай болно.
тэнцүү. KM шулуунтай перпендикуляр AB, CD, EF /Зур. 12/ шулуунууд нь өөр хоорондоо паралель байна. Паралель хоёр шулуунтай перпендикуляр шулууны урт нь паралель шулуунуудын хоорондын зай болно. илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.