Бид Давхар хүүнүүд нийтлэлд хүүний давхарлалтын талаар үзсэн. Энэ удаад давхар хүүнүүдийн өөр байрлалуудыг авч үзье.
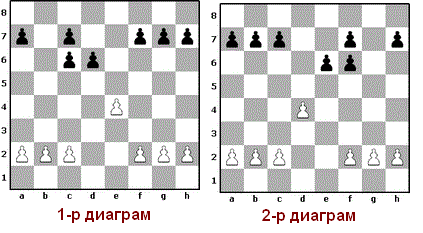 |
Хүүнүүдийн ийм байрлалын хувьд c6 эсхүл f6 хүүнүүдэд алдагдсан төвийн зарим нэгэн нөхөлт бий. Өөрөөр хэлбэл 2-р диаграмд цагаан e5 нүдэнд хамгаалагдсан байрлал буюу порпост үүсгэж чадахгүй тул хүүнүүд төвд нөлөө үзүүлдэг. Нөгөө талаас e6-e5 гэх аюултай бөгөөд эцэст нь хар f6-f5 гээд Трg8 гэж тоглож болно. Хэрвээ үүний эсрэг g2-g3 гэвэл h7-h5, f5-f4, h5-h4 гэнэ. Өөрөөр хэлбэл e6, f7, f6 хүүнүүдийн идэвхигүй масс нээгдэн дайралтад орох болно. Сул тал нь h7 тасархай хүүнд оршино. Харын Трg8, f6-f5, h7-h5 ажиллагааны хариуд цагаан хүүнүүдээ f4, g3, h2 харин морио боломжоороо f3, g2 дээр сөргүүлэн тавихыг эрмэлзэнэ. Энэ тохиолдолд тоглолт тэнцвэржинэ. |
Гэхдээ хард хамгаалалтаас дайралтад шилжих тохирох үеийг олоход маш хүндрэлтэй. Үүнийг жишээн дээр харцгаая.






 тэгшитгэлийг бод.
тэгшитгэлийг бод.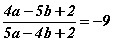 бол
бол 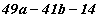 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.