Шатрын онолын мэдлэгээ бататгах хамгийн сайн арга бол мастеруудын өргийг судлах. Дөрвөн морины гарааны жишээ өргүүдэд мастерууд хэрхэн тоглож байгааг сайн судлан суралцаарай.
Шатар бол оюуны гимнастик гэдэг. Иймээс хүн бүр шатарчин болох албагүй ч энэхүү гайхамшигтай тоглоомыг тоглож чаддаг байх нь чухал. Ялангуяа хүүхэд багачууд шатар тоглож сурах нь тэдний сурлага, хүмүүжилд их сайн нөлөө үзүүлдэг тул манай ЕБС-ийн хичээлийн программд шатрын хичээлийг оруулахаар болсон байх. Гэхдээ шатрыг заавал багшаар заалгах албагүй. Өөрөө сурах бүрэн боломжтой. Яг тогтсон тодорхой дүрэмтэй тул буруу сурна гэсэн ойлголт байхгүй. Шатраар тууштай хичээллэж амжилт гаргахын тулд танд бүр хувийн дасгалжуулагч багш хэрэгтэй болно. Анхан шатны мэдлэгийг өөрөө сурахад ямарч асуудалгүй.
Танд амжилт хүсье
Нээгдсэн тоо: 1141 Төлбөртэй
Нээгдсэн тоо: 1086 Төлбөртэй
XVI -р зууны Полериогийн гар бичмэлүүдэд анхны судалгаанууд байдаг эртний гараануудын нэг. Гарааны боловсруулалтад Л. Паульсен, А. Рубинштейн, Ф. Маршалл нар их хувь нэмэр оруулсан. Гараагаар Э. Ласкер, Х. Р. Капабланка, М. Ботвинник зэрэг дэлхийн аваргууд өрөгтөө нэг бус удаа тоглосон байдаг. Гараанд байрлалын тайван тоглолтонд хүргэдэг симметр системийн зэрэгцээ хурц үргэлжлэлийг ч боловсруулсан. Өнөө үед тоглолтод гараа ховор харагдах болсон.
Дөрвөн морины гараа 1. e4 e5 2. Мf3 Мc6 3. Мc3 Мf6 нүүдлүүдийн дараагаар үүсдэг бөгөөд 4. Тb5 үргэлжлэлийг Дөрвөн морины гараа. 4. Тb5 үргэлжлэл хичээлд 4. Мd4 үргэлжлэлийг Дөрвөн морины гараа. 4. Мd4 үргэлжлэл үзсэн бол энэ удаад Белградын гамбит гэдэг 5. Мd5 үргэлжлэлийг харцгаая. Гарааны онолд суралцах нь шатрыг ул суурьтай сурах үндэс болдог.
Нээгдсэн тоо: 1263 Нийтийн
XVI -р зууны Полериогийн гар бичмэлүүдэд анхны судалгаанууд байдаг эртний гараануудын нэг. Гарааны боловсруулалтад Л. Паульсен, А. Рубинштейн, Ф. Маршалл нар их хувь нэмэр оруулсан. Гараагаар Э. Ласкер, Х. Р. Капабланка, М. Ботвинник зэрэг дэлхийн аваргууд өрөгтөө нэг бус удаа тоглосон байдаг. Гараанд байрлалын тайван тоглолтонд хүргэдэг симметр системийн зэрэгцээ хурц үргэлжлэлийг ч боловсруулсан. Өнөө үед тоглолтод гараа ховор харагдах болсон.
Дөрвөн морины гараа 1. e4 e5 2. Мf3 Мc6 3. Мc3 Мf6 нүүдлүүдийн дараагаар үүсдэг бөгөөд 4. Тb5 үргэлжлэлийг Дөрвөн морины гараа. 4. Тb5 үргэлжлэл хичээлд үзсэн бол энэ удаад4. Мd4 үргэлжлэлийг харцгаая.
Нээгдсэн тоо: 856 Төлбөртэй
Шатрын онолын мэдлэгээ бататгах хамгийн сайн арга бол мастеруудын өргийг судлах бөгөөд энэ удаад Хоёр морины гараагаар мастерууд хэрхэн тоглосон жишээг харцгаая. Практик бол ямар ч ажлыг сайн сурах хамгийн шалгарсан зам гэдгийг бүгдээрээ мэддэг ч энэ тал дээрээ хүмүүс залхуурах, хойш суух гээд дутагдалтай.
Бид амьдралдаа ихэнх зүйлийг өөрөө бие даан сурдагт дадлага, практик л голлох үүргийг гүйцэтгэдэг. Хүмүүс авьяас чадвар, хүсэл, сонирхолдоо хөтлөгдөн ямар нэгэн зүйлд суралцаж эхэлдэг ч тухайн хүнээс нилээдгүй тэсвэр хатуужил, хүч хөдөлмөр, цаг хугацаа, хөрөнгө мөнгө шаарддаг зүйл. Үүнийг дутуу ойлгосноос болоод бид өнөөдөр маш их нөөц боломжоо хий дэмий үрсээр л байх шиг санагддаг. Хүч хөдөлмөр, хөрөнгө мөнгөө зөв удирдаж сурахад манай сайт танд бага ч гэсэн туслах зорилготой. Та сайтаас өөрийн төлсөн төлбөрийн хэмжээтэй дүйцэхүүц мэдлэг, мэдээллийг олон мэдсэн бол таны ч болоод бидний зорилго биелэгдэнэ. Та зорилгодоо хүрсэн бол бидний хөдөлмөрийг зүй ёсоор үнэлэнэ гэдэгт эргэлзэхгүй байна.
Нээгдсэн тоо: 1102 Төлбөртэй
Дөрвөн морины гараа нь XVI -р зууны Полериогийн гар бичмэлүүдэд анхны судалгаанууд байдаг эртний гараануудын нэг. Гарааны боловсруулалтад Л. Паульсен, А. Рубинштейн, Ф. Маршалл нар их хувь нэмэр оруулсан. Гараагаар Э. Ласкер, Х. Р. Капабланка, М. Ботвинник зэрэг дэлхийн аваргууд өрөгтөө нэг бус удаа тоглосон байдаг. Гараанд байрлалын тайван тоглолтонд хүргэдэг симметр системийн зэрэгцээ хурц үргэлжлэлийг ч боловсруулсан. Өнөө үед тоглолтод гараа ховор харагдах болсон.
Шатарыг боломжийн хэмжээнд цаашлаад тамирчны зэрэгт хүрч сурахаар хичээж байгаа хүмүүс гарааны онолыг мэдэн судлах зайлшгүй шаардлагатай. Сонирхогчдын тухайд бол гарааны арваад нүүдэлд аль нэг нь алдаа хийснээр тоглолтын хувь заяа шийдэгдэх нь элбэг байдаг. Энэ нь сонирхогчид гарааны онолд нэг их ач холбогдол өгдөггүйтэй холбоотой. Хэрвээ та сайтад тавигдаж байгаа шатрын гараануудын хичээлүүдийг сайтар ойлгон судалбал жирийн нэгэн сонирхогчоос өөр түвшинд хүрнэ гэдэгт итгээрэй.
Нээгдсэн тоо: 958 Төлбөртэй
Хоёр морины хамгаалалт 1. e2-e4 e7-e5 2. Мg1-f3 Мb8-c6 3. Тf1-c4 Мg8-f6 нүүдлүүдээр эхэлдэг. Гарааны анхны анализ 16-р зууны үеийн Полериогийн гар бичмэлүүдэд байдаг. Гараа хоёр талд олон тооны боломжуудыг өгдөг учраас өнөө үед ч гроссмейстерүүдийн тоглолтуудад багагүй ашиглагддаг. Гарааг П. Морфи, В. Стейниц, А. Алехин зэрэг шатарчид амжилттай хэрэглэж байсны дээр Михаил Чигорин гарааны онолд их хувь нэмрийг оруулсан.
Хоёр морины хамгаалалтад хар эхний нүүдлүүдээр санаачлагыг авахыг эрмэлздэг. Ихэнх тохиолдолд харилцан нарийн төвөгтэй байрлал үүсдэг. Гарааны судалгаанд эрт үеийн болоод өнөөгийн мастеруудын олон бүтээл зориулагдсан. Зарим нэгэн хувилбарт 20-25 нүүдэл хүртэл боловсруулагдсан байдаг. Хичээлээр гарааны 4.d4 үргэлжлэлийг авч үзье. 4.Мg5 үргэлжлэлийг өмнө нь үзсэн.
Нээгдсэн тоо: 1296 Төлбөртэй
Шатрын онолын мэдлэгээ бататгах хамгийн сайн арга бол мастеруудын өргийг судлах. Эвансын гамбитийн жишээ өргүүдэд мастерууд хэрхэн тоглож байгааг сайн судлан суралцаарай.
Нээгдсэн тоо: 1159 Төлбөртэй
Хоёр морины хамгаалалт 1. e2-e4 e7-e5 2. Мg1-f3 Мb8-c6 3. Тf1-c4 Мg8-f6 нүүдлүүдээр эхэлдэг. Гарааны анхны анализ 16-р зууны үеийн Полериогийн гар бичмэлүүдэд байдаг. Гараа хоёр талд олон тооны боломжуудыг өгдөг учраас өнөө үед ч гроссмейстерүүдийн тоглолтуудад багагүй ашиглагддаг. Гарааг П. Морфи, В. Стейниц, А. Алехин зэрэг шатарчид амжилттай хэрэглэж байсны дээр Михаил Чигорин гарааны онолд их хувь нэмрийг оруулсан.
Хоёр морины хамгаалалтад хар эхний нүүдлүүдээр санаачлагыг авахыг эрмэлздэг. Ихэнх тохиолдолд харилцан нарийн төвөгтэй байрлал үүсдэг. Гарааны судалгаанд эрт үеийн болоод өнөөгийн мастеруудын олон бүтээл зориулагдсан. Зарим нэгэн хувилбарт 20-25 нүүдэл хүртэл боловсруулагдсан байдаг.
Нээгдсэн тоо: 1119 Нийтийн
1842 -1845 онуудад захидалаар Париж - Будапешт хотуудын хооронд тоглогдсон өрөгт Унгарын нийслэл ялснаар гарааны нэрийг авсан. Гарааны санаа нь итал өрөг эсхүл хоёр морины хамгаалалтад гардаг хурц, шууд хувилбаруудаас зайлсхийхэд оршино. Гараанд хар нилээд шахагдсан байрлалтай болох ч илт сул талгүй. Тэмцэл эхний нүүдлүүдээс л маневрийн шинжтэй явагддаг.
Нээгдсэн тоо: 1182 Нийтийн
Гарааг 1824 онд английн шатарчин Д.Эванс зохиосон. Эвансын гамбит нь хурц тэмцэлтэй, хоёр талд харилцан боломжууд бүхий сонирхолтой, нарийн гараа. Гарааг А.Андерсен, П.Морфи, М.Чигорин нарын мастерууд тоглолтод чадамгай ашигласан байдаг. Орчин цагт гроссмейстер Е.Свешников болон дэлхийн 13 дахь аварга Г.Каспаров зэрэг олон шатарчдын хүчин зүтгэлээр Эвансын гамбит томоохон тэмцээнүүдэд харагдах болсон.
Хар 5... Тc5 эсхүл 5... Тa5 эсхүл 5... Тe7 гэж тоглож болохыг үзсэн.
Энэ удаад 4... Тb6 гэж гамбитаас татгалзах буюу Татгалзсан Эвансийн гамбитийг авч үзье.





 тэгшитгэлийг бод.
тэгшитгэлийг бод.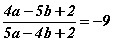 бол
бол 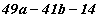 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.