a=1,(4) бутархайг энгийн бутархай болго.
Дараалал прогресс ( 130 )
Дараалал прогресс сэдвээс бодлого ороогүй шалгалт гэж бараг байхгүй байдаг. Энэ сэдэв цаашлаад анализын эхлэл болох тул сайтар ойлгосон байх хэрэгтэй. Ухагдхуунаа сайн ойлгоод хэдэн чухал томьёонуудыг мэдэж байвал бодлогууд нэг их хүнд биш. Дарааллын талаарх мэдлэг нь зарим төрлийн бодлогыг бодоход нэн хэрэгтэй болдог. Жишээ нь ердийн илэрхийллүүд дараалал байдлаар өгөгдсөн бодлогууд ихээр байдаг ч түүнийг бодлогын нөхцөлд дараалал гэдгийг заагаагүй байх гэх мэтээр
Нээгдсэн тоо: 1662 Төлбөртэй
Өсөх геометр прогресс үүсгэх гурван тооны 3 дахь нь 12 -той тэнцүү. Хэрвээ 12-ыг 9 -өөр соливол эдгээр гурван тоо нь арифметик прогресс үүсгэх бол тоонуудын нийлбэрийг ол.
Нээгдсэн тоо: 1438 Төлбөртэй
Арифметик прогрессын ялгавар тэгтэй тэнцүү биш. Энэхүү прогрессын 1-р гишүүнийг 2-р гишүүнээр, 2-р гишүүнийг 3-р гишүүнээр, 3-р гишүүнийг 1-р гишүүнээр үржүүлэхэд гарах тоонууд өгөгдсөн дарааллаар геометрийн прогресс үүсгэдэг бол геометр прогессын хуваарийг ол.
Нээгдсэн тоо: 1349 Төлбөртэй
a1=4, S5=40 байх арифметик прогрессийн d=q, a1=b1 нөхцөлийг хангах геометр прогрессийн 5-р гишүүнийг ол.
Нээгдсэн тоо: 1363 Төлбөртэй
Эхний гишүүн a1=3, ялгавар d=7 байх (an) арифметик прогресс ба a0=5 тооны хувьд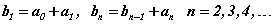 
дараалал үүсгэвэл 
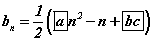байх ба 225 түүний 
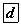дугаар гишүүн байна.
Нээгдсэн тоо: 1661 Төлбөртэй
(an) -арифметик прогрессийн хувьд a1-1, a2-2, a3-3 тоонууд геометр прогресс үүсгэх ба мөн a1-1, a2-3, a3-6 тоонууд геометр прогресс үүсгэдэг бол (an) -арифметик прогрессийн
- ялгавар нь
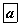
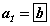
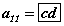байна.
Нээгдсэн тоо: 1328 Бүртгүүлэх
Арифметик прогрессийн эхний гишүүн нь -27, ялгавар нь 5 бол эхний n гишүүний нийлбэрийн хамгийн бага утгыг ол.
Нээгдсэн тоо: 1472 Бүртгүүлэх
Арифметик прогрессийн 1 ба 3-р гишүүн, геометр прогрессийн 1 ба 3-р гишүүнтэй харгалзан тэнцүү. Арифметик прогрессийн 1-р гишүүн 4, түүний 2-р гишүүн геометр прогрессийн 2-р гишүүнээс 32 -оор илүү, энэ хоёр прогрессийн бүх гишүүд эерэг бол арифметик прогрессийн ялгаврыг ол.
Нээгдсэн тоо: 1251 Төлбөртэй
b1 ; b2 ; b3 ; b4 тоонууд геометр прогрессын дараалсан гишүүд ба харгалзан 6 ; 7 ; 6 ; 1 -ийг нэмбэл арифметик прогресс үүснэ. b1 + b2 + b3 + b4 нийлбэрийг ол.
Энэ долоо хоногт
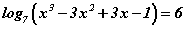тэгшитгэлийг бод.