Суурь нь P периметртэй, диагоналууд хоорондын хурц өнцөг нь α -тай тэнцүү тэгш өнцөгт пирамидийн бүх хажуу ирмэгүүд суурийн хавтгайд β өнцгөөр налсан бол пирамидийн эзэлхүүн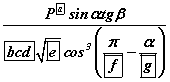 
байна.
Огторгуйн геометр ( 103 )
Ерөнхий боловсролын сургуулийн хэмжээнд цэвэр огторгуйн геометрийн бодлогууд ордоггүй. Зөвхөн хавтгайн гурван хэмжээст орон зайн бодлогууд байдаг. Ийм төрлийн бодлогыг бодохдоо зургийг маш сайн ойлгон зурж сурах нь хамгийн чухал. Зураглалыг сайн гаргаж чадвал бодлогыг бодоход амархан болдог.
Нээгдсэн тоо: 444 Төлбөртэй
Нээгдсэн тоо: 726 Төлбөртэй
Зөв дөрвөн өнцөгт QABCD пирамидийн өндөр ба суурийн талууд a бол QCD хавтгай AB шулуун хоорондын зай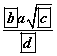 
байна.
Нээгдсэн тоо: 1019 Төлбөртэй
Зөв ABCA1B1C1 гурвалжин призмийн өндөр суурийн талтай тэнцүү бол AB1 диагонал болон AA1C1C хавтгай хоорондын өнцгийг ол.
Нээгдсэн тоо: 2092 Нийтийн
Зөв тетраэдрийн ирмэг болон тухайн ирмэгийг агуулаагүй хавтгай хоорондын өнцгийг ол.
Нээгдсэн тоо: 946 Төлбөртэй
SABC пирамидийн өндөр SH нь AB талын дунд бууна. Пирамидийн суурь ABC зөв гурвалжны тал 6 бөгөөд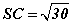 
бол пирамидийн эзэлхүүнийг ол.
Нээгдсэн тоо: 987 Төлбөртэй
ABCD ромбо суурьтай S оройтой SABCD пирамид өгөгджээ. Пирамидийн өндөр SO суурийн ромбийн диагоналуудийн огтлолцол дээр бууна. ASO өнцөг SBO өнцөгтэй тэнцүү ба суурийн диагоналуудын урт 6, 24 бол пирамидийн эзэлхүүнийг ол.
Нээгдсэн тоо: 711 Төлбөртэй
Зөв дөрвөн өнцөгт пирамидын хажуу талс суурьтай 600 өнцөг үүсгэнэ. Суурийн тал 4 нэгж бол хажуу ирмэгийн уртыг ол.
Нээгдсэн тоо: 433 Бүртгүүлэх
Огтлогдсон конусийн суурийн радиусууд 3 м ба 9 м өндөр нь 8 м бол хажуу гадаргуугийн талбайг олоорой.
Нээгдсэн тоо: 7163 Нийтийн
Цилиндрийн суурийн радиус 2 дм, өндөр нь 4 дм бол тэнхлэг огтлолын талбай нь хэдэн дм.кв вэ?
Нээгдсэн тоо: 1359 Төлбөртэй
Суурийн талбай нь 8 , хажуу ирмэг нь 6 -тай тэнцүү ABCA1B1C1 зөв гурвалжин призм өгөгджээ. Призмийн ACA1B1C1 оройнуудад оройтой олон талстын эзэлхүүнийг ол.
Энэ долоо хоногт
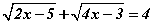тэгшитгэл бод.
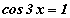тэгшитгэл бод.
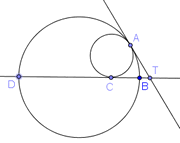Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Нээгдсэн тоо : 1065