Бөмбөрцөгт багтсан зөв гурвалжин пирамидын суурь нь бөмбөрцгийн төвийг дайрч байв. Бөмбөрцгийн радиус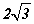 
тай тэнцүү. Пирамидын эзэлхүүнийг ол.
Огторгуйн геометр ( 103 )
Ерөнхий боловсролын сургуулийн хэмжээнд цэвэр огторгуйн геометрийн бодлогууд ордоггүй. Зөвхөн хавтгайн гурван хэмжээст орон зайн бодлогууд байдаг. Ийм төрлийн бодлогыг бодохдоо зургийг маш сайн ойлгон зурж сурах нь хамгийн чухал. Зураглалыг сайн гаргаж чадвал бодлогыг бодоход амархан болдог.
Нээгдсэн тоо: 1536 Төлбөртэй
Нээгдсэн тоо: 1567 Төлбөртэй
A; B; C цэгүүд бөмбөрцөг дээр байрлах ба төвөөс (ABC) хавтгай хүрэх зай 12м. AB=6м; BC=8м; AC=10м бол бөмбөрцгийн гадаргуугийн талбайг ол.
Нээгдсэн тоо: 3198 Төлбөртэй
Кубын гол диагональ 10 см бол эзэлхүүнийг ол.
Нээгдсэн тоо: 1471 Төлбөртэй
SABC пирамидын ASB, ASC өнцгүүд нь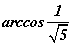 
. BSC өнцөг тэгш, SB=a болно. Тэгвэл 
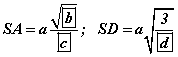байна.
Нээгдсэн тоо: 1258 Төлбөртэй
ABCDA1B1C1D1 призмийн суурь нь ABCD (AD || BC) адил хажуут трапец болно. AA1D1D хавтгайд төвтэй 3 радиустай бөмбөрцөг нь ABCD , A1B1C1D1 хавтгайнууд болон AA1 , BB1 , CC1 , DD1 шулуунуудыг шүргэнэ. A1D1=7, BC=5 бол
- AD, BB1 гийн хоорондох өнцөг
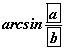
- Призмийн эзэлхүүн
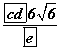байна.
Нээгдсэн тоо: 1880 Төлбөртэй
KLM суурьтай, KL=1, KK1=d талтай KLL1K1 тэгш өнцөгт хажуу бүхий KLMK1L1M1 призм өгөгджээ. KL_|_KM, LMM1 , KMM1 хавтгайнуудын хоорондын өнцөг 60°,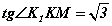 
бол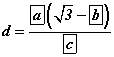 
утганд призмд түүний бүх талыг шүргэх шаарыг багтааж болно.
Нээгдсэн тоо: 1557 Төлбөртэй
Конусын байгуулагч ба суурь хоорондын өнцөг 30°. R - конусыг багтаасан шаарын радиус, r - конуст багтсан шаарын радиус бол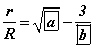 
байна.
Нээгдсэн тоо: 1507 Төлбөртэй
Зөв гурвалжин пирамидадын апофемуудын хоорондох өнцөг 90° харин хажуу ирмэг l=6 тэнцүү бол пирамидын хажуу гадаргуун талбай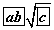 
байна.
Нээгдсэн тоо: 1606 Төлбөртэй
Өндөр нь h=6 -тай тэнцүү зөв гурвалжин пирамидад R=2 радиустай шаар багтжээ. Пирамидын суурийн талыг ол.
Нээгдсэн тоо: 4027 Нийтийн
Зэрэгцээ орших ирмэгүүд нь оройдоо 60° өнцөг үүсгэсэн 3 өндөртэй зөв дөрвөн өнцөгт пирамидын эзэлхүүн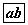 
тэнцүү.
Энэ долоо хоногт
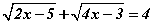тэгшитгэл бод.
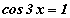тэгшитгэл бод.
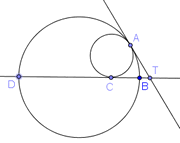Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Нээгдсэн тоо : 1065