ABC зөв гурвалжин суурьтай SABC пирамидын суурийн талууд нь 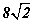 см, SC хажуу ирмэгийн урт нь 8 см бөгөөд суурийн хавтгайд перпендикуляр байв. S орой ба BC талын дундаж цэгийг дайрсан шулуун, AB талын дундаж цэг ба C оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондын зайг олоорой.
см, SC хажуу ирмэгийн урт нь 8 см бөгөөд суурийн хавтгайд перпендикуляр байв. S орой ба BC талын дундаж цэгийг дайрсан шулуун, AB талын дундаж цэг ба C оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондын зайг олоорой.
Бодолт:
AB, BC талын дундаж цэгүүдийг харгалзан D, E гэе. AB шулууныг агуулсан, CD шулуунд перпендикуляр хавтгайд SABC пирамидыг проекцлон CD хэрчим D' цэгт, E цэг E' цэгт, S цэг S' цэгт тус тус буусан гэж үзвэл 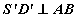 ба S'D'=8 болно. Бидний олох ёстой 2 шулууны хоорондох зай нь S'D'E' гурвалжны S'E' гипотенуз дээр буусан D'H өндөр юм.
ба S'D'=8 болно. Бидний олох ёстой 2 шулууны хоорондох зай нь S'D'E' гурвалжны S'E' гипотенуз дээр буусан D'H өндөр юм. 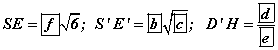 .
.
Олох ёстой өнцгөө α гэж тэмдэглэвэл 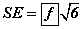 тул
тул 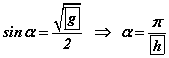 байна.
байна.





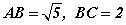 талуудтай ABCD тэгш өнцөгт. Харин пирамидын хажуу ирмэгүүд
талуудтай ABCD тэгш өнцөгт. Харин пирамидын хажуу ирмэгүүд 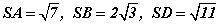 бол SA -г пирамидын өндөр гэдгийг батлаад SC шулуун болон ASB хавтгай хоорондох өнцгийг ол.
бол SA -г пирамидын өндөр гэдгийг батлаад SC шулуун болон ASB хавтгай хоорондох өнцгийг ол.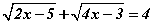 тэгшитгэл бод.
тэгшитгэл бод.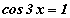 тэгшитгэл бод.
тэгшитгэл бод.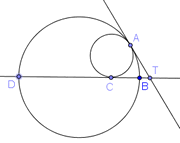 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.