Теорем, аксиом, тодорхойлолт
Баталгаа - Ямар нэгэн шинж чанарыг тогтоохыг хэлэлцэх.
Теорем - Баталгаа шаардсан ямар нэгэн шинж чанарыг тогтоохыг нотлох. Теоремуудыг бас лемм, шинж, үр дагавар, дүрэм, чанар, нотолгоо гэж нэрлэдэг. Теоремыг өмнө нь тогтоосон шинжүүдийг үндэслэн баталдаг. Геометрт зарим шинж чанарыг үндсэн гэж үзэж баталгаа шаардахгүй хэрэглэдэг.
Аксиом - Баталгаагүйгээр ашигладаг зарим шинж чанарыг тогтоосон нотолгоо. Аксиом нь туршилтаас үүсдэг бөгөөд туршилт нь тэдгээрийн үнэнийг бүхэлд нь тогтооно.Янз бүрийн аргаар аксиомуудыг зохиож болно. Гэхдээ аксиом нь геометрийн бусад шинж чанарыг батлахад хангалттай байх хэрэгтэй. Нэг аксиомыг нөгөөгөөр соливол энэ нь теорем болж байгаа тул түүнийг батлах хэрэгтэй болдог.
Математикийн хичээлийн бүх сэдвийг хамарсан ерөнхий курсын хичээлүүд. Та математикийн хичээлээ давтах, бодлого бодох, шалгалтанд бэлтгэхийн тулд ерөнхий ухагдхуун, үндсэн зарчмуудын талаар тодорхой хэмжээний мэдлэгтэй байх хэрэгтэй. Манай сайтын энэ хэсэгт математикийн хичээлтэй холбогдолтой онолын материалуудыг нийтлэж байх тул эндээс та өөртөө хэрэгтэй мэдээллийг олон авна гэдэгт итгэж байна.
Танд амжилт хүсье.
Нээгдсэн тоо: 6888 Нийтийн
Нээгдсэн тоо: 8387 Төлбөртэй
Сэлгэмэл
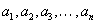 гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг сэлгэмэл гэнэ. n элементээс гаргах сэлгэмэлийн нийт тоог Pn гэж тэмдэглэнэ. Энэ тоо нь 1 ээс n хүртэлх бүх тоонуудын үржвэртэй тэнцүү байдаг.
гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг сэлгэмэл гэнэ. n элементээс гаргах сэлгэмэлийн нийт тоог Pn гэж тэмдэглэнэ. Энэ тоо нь 1 ээс n хүртэлх бүх тоонуудын үржвэртэй тэнцүү байдаг.
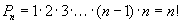
1·2·3·…·( n−1 )·n үржвэрийг хураангуй байдлаар n! гэж тэмдэглэдэг бөгөөд факториал гэж нэрлэдэг. 0!=1 байдаг.
Жишээ:
a, b, c гэсэн 3 элементээс гарах сэлгэмэлийн тоог ол.
Бодолт:
Сэлгэмэлийн тоог олох томьёогоор 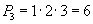 болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.
болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.
Нээгдсэн тоо: 4555 Бүртгүүлэх
Логарифмын үндсэн адитгал
N эерэг тооны (b>0,b≠1) суурьтай логарифм гэдэг нь N ийг гаргах b гийн x зэрэг илтгэгчийг хэлнэ. Логарифмыг доорх байдлаар тэмдэглэнэ.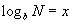 Энэ бичлэг нь
Энэ бичлэг нь 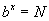 гэсэнтэй адил.
гэсэнтэй адил.
Жишээ: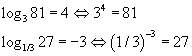
Логарифмын тодорхойлолтыг 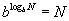 адитгал байдлаар бичиж болно.
адитгал байдлаар бичиж болно.
Нээгдсэн тоо: 7506 Бүртгүүлэх
Натурал тоон цувааг авч үзье.
1, 2, 3, … ,n-1, n, …
Энэ цувааны тоо бүрийг тодорхой дүрмийн дагуу un тоогоор соливол бид шинэ тоон цувааг гаргана
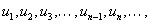
Энэ шинэ гарсан цувааг тоон дараалал гэдэг. un тоог тоон цувааны ерөнхий гишүүн гэнэ.
Тоон цувааны жишээнүүд
2, 4, 6, … , 2n, …;
1, 4, 9, 16, 25, … , n², …;
1, 1/2, 1/3, 1/5, … , 1/n, …;
Нээгдсэн тоо: 2653 Төлбөртэй
Тэнцэл бишийн баталгаа
Тэнцэл бишийг батлах хэд хэдэн арга байдаг. Эдгээрийг 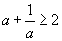 / энд a эерэг тоо / жишээн дээр авч үзье.
/ энд a эерэг тоо / жишээн дээр авч үзье.
1. Мэдэгдэж буй эсвэл өмнө нь батлагдсан тэнцэл бишийг ашиглах.
( a−1 )2 ≥0 гэдэг нь ойлгомжтой. a>0 учраас 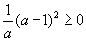 байна. Хаалтыг задалбал
байна. Хаалтыг задалбал 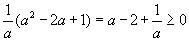 болох бөгөөд эндээс
болох бөгөөд эндээс 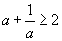 гарна.
гарна.
2. Тэнцэл бишийн хэсгүүдийн ялгаварын тэмдгийг ашиглах.
Тэнцэл бишийн зүүн баруун талын хэсгийн ялгаварыг авч үзье. 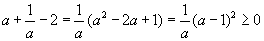 Эндээс a=1 үед л тэнцэл гарах нь харагдаж байна.
Эндээс a=1 үед л тэнцэл гарах нь харагдаж байна.
3. Эсрэгээс нь батлах.
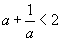 гэж үзье. Тэнцэл бишийн хоёр талыг a гаар үржүүлбэл a2 +1<2a буюу a2 +1−2a<0 өөрөөр (a−1)2 <0 болно. Энэ нь буруу тэнцэл биш тэгэхээр эсрэг тохиолдол нь үнэн болно.
гэж үзье. Тэнцэл бишийн хоёр талыг a гаар үржүүлбэл a2 +1<2a буюу a2 +1−2a<0 өөрөөр (a−1)2 <0 болно. Энэ нь буруу тэнцэл биш тэгэхээр эсрэг тохиолдол нь үнэн болно.
Нээгдсэн тоо: 2402 Бүртгүүлэх
(>) их , (<) бага , (≥) их буюу тэнцүү , (≤) бага буюу тэнцүү тэмдгүүдийн аль нэгээр холбогдсон тоон болон үсгэн илэрхийллүүд тэнцэл биш үүсгэнэ. Тэнцэл бишид орсон үсгэн хэмжээнүүд нь тодорхой болон үл мэдэгдэгч байдлаар байж болно. Тэнцэл бишийг бодох гэдэг нь тэнцэл бишийг үнэн байлгах үл мэдэгдэгчийн утгуудын хилийг олохыг хэлнэ. Тэнцэл бишийн системийг бодох гэдэг нь системд орсон тэнцэл бишүүдийг нэгэн зэрэг үнэн байлгах үл мэдэгдэгчдийн утгуудын хилийг олохыг хэлнэ.
Нээгдсэн тоо: 12073 Нийтийн
Натурал n тооноос хамаарсан тодорхой шинжийг батлах хэрэгтэй боллоо гэж бодъё. Энэ шинж нь томьёо, адитгал, тэнцэл биш, нотолгоо байж болно. Хэрвээ
Энэ шинж ямар нэгэн n0 натурал тооны хувьд үнэн
n=k үед энэ шинж үнэн байх нөхцлөөс үүдэн дурын k≥ n0 хувьд n=k+1 үед энэ шиж үнэн гэвэл энэ шинж нь дурын n≥ n0 натурал тооны хувьд үнэн байна.
Жишээ:
1+3+5+ … +(2n-1)=n² гэдгийг батал.
Нээгдсэн тоо: 14449 Төлбөртэй
Квадрат тэгшитгэлийн бодолтын D<0 / энд D нь квадрат тэгшитгэлийн дискриминант / үед шинэ төрлийн тооны хэрэгцээ гарч ирсэн. Удаан хугацаанд эдгээр тоонуудыг бодит хэрэгцээ гараагүй байснаас тэдгээрийг хуурмаг тоо гэж нэрлэж байлаа. Одоо эдгээр тоо нь физик, цахилгаан техник, аэро болон гидродинамикт зэрэгт маш өргөн хэрэглэгээтэй болсон. Комплекс тоог a+bi хэлбэрээр бичдэг. Энд a ба b нь бодит тоо, харин i нь хуурмаг нэг буюу i²=-1. a тоог комплекс тооны абсцисс, харин b тоог ординат гэдэг. a+bi ба a-bi хоёр комплекс тоог хос комплекс тоо гэдэг.
Үндсэн тохиролцоо
- Бодит a тоог a+0i эсвэл a-0i гэсэн комплекс хэлбэрээр бичиж болно. Жишээ : 5+0i эсвэл 5-0i бичлэг нь 5 гэсэн тоог илэрхийлнэ.
- 0+bi комплекс тоог цэвэр хуурмаг тоо гэнэ. bi бичлэг нь 0+bi гэснийг илэрхийлнэ.
- a+bi ба c+di хоёр комплекс тооны a=c , b=d байвал эдгээр тоог тэнцүү гэнэ. Эсрэг тохиолдолд комплекс тоонуудыг тэнцүү биш гэнэ
Нээгдсэн тоо: 7960 Төлбөртэй
Хавтгай буюу огторгуйд байрлах хоёр цэгийг холбосон чиглэл бүхий хэрчмийг вектор гэнэ. Векторыг голдуу жижиг үсэг эсвэл эхлэл төгсгөлийн цэгүүдээр тэмдэглэж дээр нь зураас тавьдаг.
Жишээ нь A цэгээс B цэг рүү чиглэсэн векторыг 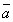 эсвэл
эсвэл 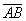 гэж тэмдэглэнэ.
гэж тэмдэглэнэ.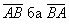 векторуудыг эсрэг вектор гэнэ. Тэгвэл
векторуудыг эсрэг вектор гэнэ. Тэгвэл 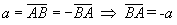 болно.
болно.
Эхлэл төгсгөлийн цэг нь давхцаж байгаа векторыг тэг вектор гэдэг бөгөөд 0 эсвэл 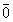 гэж тэмдэглэнэ.
гэж тэмдэглэнэ.
Векторыг үзүүлж байгаа AB хэрчмийн уртыг векторын урт /модуль/ /тэмдэглэгээ |a| / гэнэ.
Хэрвээ векторуудын чиглэл заасан хэрчмүүд паралел шулуун дээр байвал тэдгээрийг коллинар вектор гэдэг. a, b векторуудыг коллинар гэдгийг a||b гэж тэмдэглэнэ.
Гурав ба түүнээс дээш векторууд нэг хавтгайд оршиж байвал тэдгээрийг комплинар вектор гэнэ.
Нээгдсэн тоо: 3438 Төлбөртэй
1. Дээд эрэмбийн зарим тэгшитгэлийг квадрат тэгшитгэлийг ашиглан бодож болно. Тэгшитгэлийн зүүн талыг хоёроос ихгүй зэрэгтэй үржигдхүүнээр задлана. Тэгээд үржигдхүүн болгоныг тэгтэй тэнцүүлж квадрат эсвэл шугаман тэгшитгэлийг бодсноор анхдагч тэгшитгэлийн бүх шийдийг олно.
Жишээ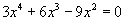 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Бодолт
Тэгшитгэлийн зүүн талыг үржвэрт задалбал.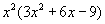 болно. Эндээс x2=0 тэгшитгэлийн шийд нь x1=x2=0 гэж гарна.
болно. Эндээс x2=0 тэгшитгэлийн шийд нь x1=x2=0 гэж гарна.
Одоо 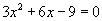 тэгшитгэлийг бодвол x3=1, x4=-3 гэж гарна
тэгшитгэлийг бодвол x3=1, x4=-3 гэж гарна
Тэгэхлээр анхны тэгшитгэл нь x1=0, x2=0, x3=1, x4=-3 гэсэн 4 шийдтэй болно.





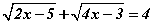 тэгшитгэл бод.
тэгшитгэл бод.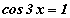 тэгшитгэл бод.
тэгшитгэл бод.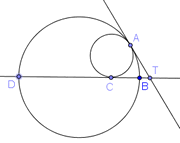 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.