Энэ хэсэгт бид хавтгай дүрсийн талбайг олоход өргөн хэрэглэдэг томьёонуудыг авч үзнэ.
Квадрат /Зур. 58/ a - тал , d - диагнал.
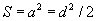
Тэгш өнцөгт /Зур. 59/ a, b - талууд.
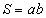
Математикийн хичээлийн бүх сэдвийг хамарсан ерөнхий курсын хичээлүүд. Та математикийн хичээлээ давтах, бодлого бодох, шалгалтанд бэлтгэхийн тулд ерөнхий ухагдхуун, үндсэн зарчмуудын талаар тодорхой хэмжээний мэдлэгтэй байх хэрэгтэй. Манай сайтын энэ хэсэгт математикийн хичээлтэй холбогдолтой онолын материалуудыг нийтлэж байх тул эндээс та өөртөө хэрэгтэй мэдээллийг олон авна гэдэгт итгэж байна.
Нээгдсэн тоо: 5134 Бүртгүүлэх
Энэ хэсэгт бид хавтгай дүрсийн талбайг олоход өргөн хэрэглэдэг томьёонуудыг авч үзнэ.
Квадрат /Зур. 58/ a - тал , d - диагнал.
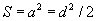
Тэгш өнцөгт /Зур. 59/ a, b - талууд.
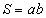
Нээгдсэн тоо: 10603 Төлбөртэй
Зөв олон өнцөгт
Өнцгүүд нь тойрог дээр байрлах олон өнцөгтийг тойрогт багтсан /Зур. 54/, талууд нь тойргийн шүргэгч болж байгаа олон өнцөгтийг тойрог багтаасан /Зур. 55/ гэж нэрлэдэг.
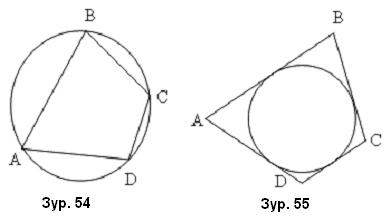
Олон өнцөгтийн орой дээгүүр дайрч өнгөрч байгаа тойргийг багтаасан тойрог /Зур. 54/, олон өнцөгтийн талууд нь шүргэгч болж байгаа тойргийг багтсан тойрог /Зур. 55/ гэж бас нэрлэдэг.
Нээгдсэн тоо: 4002 Төлбөртэй
Цэг
Цэгүүдийн геометр байрлал. – энэ нь өгөгдсөн тодорхой нөхцлийг хангах бүх цэгийн олонлог.
Жишээ 1
Дурын хэрчмийн дундажид буулгасан перпендикуляр нь энэ хэрчмийн төгсгөлүүдээс ижил зайд орших цэгүүдийн геометр байрлал / бүх цэгийн олонлог / юм. PO 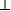 AB ба AO = OB гэе
AB ба AO = OB гэе
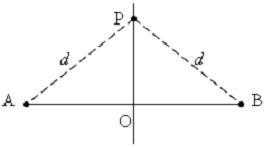
Тэгвэл дундажийн перпендикуляр дээрх дурын P цэг нь AB хэрчмийн төгсгөлүүд A , B ээс d тэй тэнцүү ижил зайд байна.
Нээгдсэн тоо: 2519 Бүртгүүлэх
Хавтгай дүрсийн бүх хэмжээг нэг ижил тоо / ихэсгэх эсвэл багасгах / дахин өөрчлөхөд гарсан дүрс анхны дүрс хоёрыг төстэй гэнэ. Хоёр төстэй дүрсийн хувьд тэдгээрийн харгалзах өнцгүүд тэнцүү. Нэг дүрс дээрх A, B, C, D цэгүүд нь нөгөө дүрс дээрх a, b, c, d цэгүүдтэй харгалзаж байвал 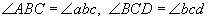 гэх мэт байна.
гэх мэт байна.
ABCDEF ба abcdef хоёр олон өнцөгт /Зур. 37/ төстэй бол, тэдгээрийн өнцгүүд тэнцүү 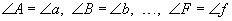 , харин талууд нь порпорционал байна.
, харин талууд нь порпорционал байна.
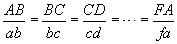
Нээгдсэн тоо: 6536 Төлбөртэй
Паралелграм ба трапец
Эсрэг талууд нь хос хосоороо паралел байдаг дөрвөн өнцөгтийг паралелграм гэнэ. /Зур. 32/
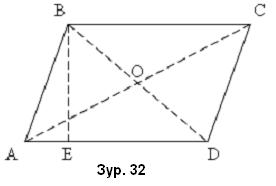
Паралелграмын эсрэг байрлах дурын хоёр талыг сууриуд гэх бөгөөд тэдгээрийн хоорондох зайг өндөр гэдэг. / BE, Зур. 32/
Нээгдсэн тоо: 9213 Төлбөртэй
Гурван талтай / эсвэл гурван өнцөгтэй / олон өнцөгтийг гурвалжин гэнэ. Гурвалжингийн талуудыг голдуу жижиг үсгээр , талын эсрэг орших оройг том үсгээр тэмдэглэдэг.
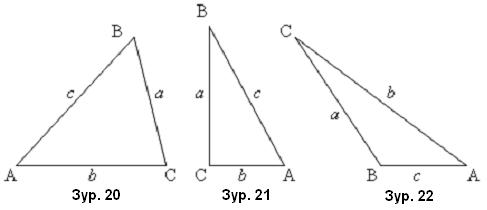
Гурвалжингийн бүх гурван өнцөг нь /Зур. 20/ хурц байвал хурц өнцөгт , аль нэг өнцөг нь 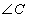 /Зур. 21/ тэгш байвал тэгш өнцөгт гурвалжин гэж нэрлэнэ. Тэгш өнцөгт гурвалжны тэгш өнцгийг үүсгэж байгаа a, b талуудыг катетууд, харин тэгш өнцгийн эсрэг орших талыг гипотенуз гэдэг. Гурвалжингийн аль нэг өнцөг нь
/Зур. 21/ тэгш байвал тэгш өнцөгт гурвалжин гэж нэрлэнэ. Тэгш өнцөгт гурвалжны тэгш өнцгийг үүсгэж байгаа a, b талуудыг катетууд, харин тэгш өнцгийн эсрэг орших талыг гипотенуз гэдэг. Гурвалжингийн аль нэг өнцөг нь 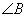 /Зур. 22/ мохоо байвал мохоо өнцөгт гурвалжин гэнэ.
/Зур. 22/ мохоо байвал мохоо өнцөгт гурвалжин гэнэ.
Нээгдсэн тоо: 23988 Нийтийн
Хэрчмүүдээр бүрэн хаагдсан хавтгай дүрсийг олон өнцөгт гэнэ. Өнцгийн тооноосоо хамааран олон өнцөгт нь гурвалжин, дөрвөлжин, таван өнцөгт, зургаан өнцөгт гэх мэтээр байж болно. /Зур. 17/ дээр ABCDEF гэсэн зургаан өнцөгтийг үзүүлсэн байна. A, B, C, D, E, F цэгүүдийг олон өнцөгтийн орой гэнэ.
Нээгдсэн тоо: 4154 Нийтийн
Хавгайн геометрт ихэнхдээ ашиглагддаг аксиомуудыг авч үзье
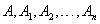 гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа
гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа 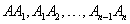 хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба
хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба 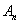 хооронд B цэг оршино.
хооронд B цэг оршино.Нээгдсэн тоо: 18991 Нийтийн
Нэг хавтгай дээр орших хоорондоо огтлолцодгүй /Зур. 11/ AB ба CD шулуунуудыг паралель шулуун гэдэг бөгөөд AB || CD гэж тэмдэглэнэ. Паралель шугамын нэг дээр байрлах цэг нөгөө шугаман дээр байрлах цэгээс ижил зайд байна. Паралель шугамын хоорондох өнцөгийг тэг гэж үздэг. Нэг чигт чиглэсэн хоёр паралель цацрагийн хоорондох өнцөг тэгтэй , эсрэг чиглэлтэй тохиолдолд 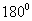 тэнцүү. KM шулуунтай перпендикуляр AB, CD, EF /Зур. 12/ шулуунууд нь өөр хоорондоо паралель байна. Паралель хоёр шулуунтай перпендикуляр шулууны урт нь паралель шулуунуудын хоорондын зай болно.
тэнцүү. KM шулуунтай перпендикуляр AB, CD, EF /Зур. 12/ шулуунууд нь өөр хоорондоо паралель байна. Паралель хоёр шулуунтай перпендикуляр шулууны урт нь паралель шулуунуудын хоорондын зай болно.
Нээгдсэн тоо: 4737 Бүртгүүлэх
O гэсэн нэг цэгээс / өнцгийн орой / гарсан OA , OB хоёр цацрагаас / өнцгийн талууд / үүссэн геометрийн дүрсийг өнцөг гэнэ. /Зур. 1/
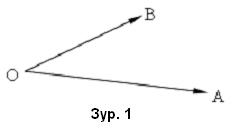
Өнгийг 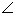 тэмдэг ба өнцгийн орой, төгсгөлүүдийг заасан 3 үсгээр
тэмдэг ба өнцгийн орой, төгсгөлүүдийг заасан 3 үсгээр 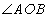 гэж тэмдэглэнэ. Ингэхдээ оройг илэрхийлэх үсгийг дунд нь бичнэ. Өнцгийг OA цацраг O оройг тойрон OB цацрагтай давхцах хүртэл эргэлтээр хэмжинэ. Радиан ба градус гэсэн хоёр нэгжийг өнцгийн хэмжээнд голлон ашигладаг.
гэж тэмдэглэнэ. Ингэхдээ оройг илэрхийлэх үсгийг дунд нь бичнэ. Өнцгийг OA цацраг O оройг тойрон OB цацрагтай давхцах хүртэл эргэлтээр хэмжинэ. Радиан ба градус гэсэн хоёр нэгжийг өнцгийн хэмжээнд голлон ашигладаг.