Тохиолдол 1.
a, b, c - талууд өгөгдсөн. A, B, C - өнцгүүдийг олох.
- Косинусын теоремоор аль нэг өнцгийг олно.
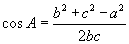
- Синусын теоремоор хоёрдох өнцгийг олно.
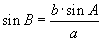
- Гуравдахь өнцгийг дараах томьёогоор олно.
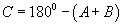
Математикийн хичээлийн бүх сэдвийг хамарсан ерөнхий курсын хичээлүүд. Та математикийн хичээлээ давтах, бодлого бодох, шалгалтанд бэлтгэхийн тулд ерөнхий ухагдхуун, үндсэн зарчмуудын талаар тодорхой хэмжээний мэдлэгтэй байх хэрэгтэй. Манай сайтын энэ хэсэгт математикийн хичээлтэй холбогдолтой онолын материалуудыг нийтлэж байх тул эндээс та өөртөө хэрэгтэй мэдээллийг олон авна гэдэгт итгэж байна.
Нээгдсэн тоо: 4388 Төлбөртэй
Тохиолдол 1.
a, b, c - талууд өгөгдсөн. A, B, C - өнцгүүдийг олох.
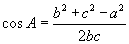
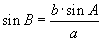
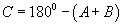
Нээгдсэн тоо: 7532 Нийтийн
Тэмдэглэгээ
a, b, c - талууд, A, B, C - өнцгүүд, p=(a+b+c)/2 - хагас периметр, h - өндөр, S - талбай, R - багтаасан тойргийн радиус, r - багтсан тойргийн радиус.
Косинусын теорем
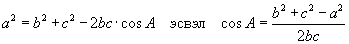
Нээгдсэн тоо: 35870 Нийтийн
Гаргалтын томьёо
Эдгээр томьёог
ашигладаг.
Нээгдсэн тоо: 3075 Төлбөртэй
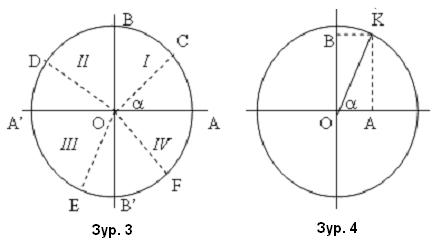
Тригнометрт дурын өнцгийн / хурц, мохоо, эерэг, сөрөг / хувьд үнэн байх дүрмийг гаргахын тулд нэгж тойрогийг байгуулах хэрэгтэй. Өөрөөр хэлбэл радиус нь 1 тэнцүү тойрог. / Зур. 3 /
Нээгдсэн тоо: 16757 Бүртгүүлэх
Хоёр талаар нь бодох.
Тэгш өнцөгт гурвалжны хоёр тал нь өгөгдсөн тохиолдолд гуравдахь талыг Пифагорын томьёогоор тооцож олно. Хурц өнцгийг ямар хоёр тал нь өгөгдсөнөөс хамаарч тохирох тригнометрийн функцийг хэрэглэнэ. Жишээ нь a, b катетууд өгөгдсөн бол A өнцгийг 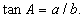 олох юм.
олох юм.
Жишээ 1
Тэгш өнцөгт гурвалжны катет a=0.324, гипотенуз c=0.544 бол b катет ба A, B өнцгийг ол.
Бодолт
Катет нь 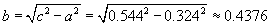 Өнцөг нь
Өнцөг нь 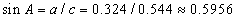 буюу
буюу 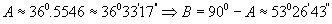 болно.
болно.
Нээгдсэн тоо: 3961 Бүртгүүлэх
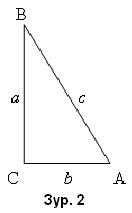
Тэгш өнцөгт гурвалжны талуудын харьцааг хурц өнцгийн тригнометрийн функцүүд гэдэг. / Зур. 2 /
Нээгдсэн тоо: 8617 Бүртгүүлэх
Бид хавтгайн геометрт нумын урт l, радиус r ба харгалзах өнцөг α -нууд нь α=l/r гэсэн харьцаатай байдгийг үзсэн. Энэ томьёо нь өнцгийн радиан хэмжээг тогтоох үндэс болно. Хэрвээ l=r бол α=1 болох бөгөөд энийг α өнцөг 1 радиантай тэнцүү гээд α=1 рад. гэж тэмдэглэнэ. Эндээс дараах тодорхойлолт гарна.
Нумын урт ба радиус нь тэнцүү төв өнцгийг радиан гэнэ. (AmB=AO) /Зур. 1/ Иймээс өнцгийн радиан хэмжээс гэдэг нь дурын радиусаар татаж гаргасан өнцгийн талуудын дунд орших нумын уртыг нумын радиуст харьцуулсан харьцааг хэлнэ.
Нээгдсэн тоо: 42830 Нийтийн
Тэмдэглэгээ:
V - эзэлхүүн ; S - суурийн талбай ; 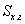 - хажуу гадаргуун талбай; P - бүтэн гадаргуу; h - өндөр; a, b, c - тэгш өнцөгт паралелпепидын хэмжээсүүд; A - зөв ба зөв зүсэгдсэн пирамидийн апофем; L - конусын бүрдүүлэгч; p - периметр эсвэл суурийн тойргийн урт; r - суурийн радиус; d - суурийн диаметр; R - шаарын радиус; D - шаарын диаметр; 1 ба 2 индексүүд нь зүсэгдсэн призм ба пирамидийн радиус, диаметр, периметр, дээд доод сууриудтай холбоотой.
- хажуу гадаргуун талбай; P - бүтэн гадаргуу; h - өндөр; a, b, c - тэгш өнцөгт паралелпепидын хэмжээсүүд; A - зөв ба зөв зүсэгдсэн пирамидийн апофем; L - конусын бүрдүүлэгч; p - периметр эсвэл суурийн тойргийн урт; r - суурийн радиус; d - суурийн диаметр; R - шаарын радиус; D - шаарын диаметр; 1 ба 2 индексүүд нь зүсэгдсэн призм ба пирамидийн радиус, диаметр, периметр, дээд доод сууриудтай холбоотой.
Нээгдсэн тоо: 2485 Нийтийн
Нэг нь нөгөөгийнхөө бүх шугаман хэмжээсийг нэг ижил харьцаагаар исэхгэх юмуу багасгах замаар гаргасан хоёр биетийг төстэй биет гэнэ. Автомашин түүний модел хоёр нь төстэй биетүүд.
Биетийн төстэй байх шинжүүд:
Нээгдсэн тоо: 6145 Төлбөртэй
Биет дээр орших E цэг бүрт энэ биет дээр E’ гэсэн цэг олдоод EE’ хэрчим нь S хавтгайтай перпендикуляр бөгөөд хавтгайгаар (EA=AE’) гэсэн тэнцүү хэсэгт хуваагдаж байвал геометрийн дүрсийг S хавтгайгаар тэгш хэмтэй /Зур. 104/ гэнэ. Нарийн утгаараа тэгш хэмтэй дүрс болон биетүүд нь өөр хоорондоо тэнцүү биш байдаг.
Жишээ нь зүүн гарын бээлий нь баруун гарт таардаггүй г.м. Эдгээрийг толин тусгалын тэнцүү гэдэг.