Хэрвээ X хэсэгт 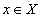 байх x болгоны хувьд
байх x болгоны хувьд 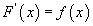 бол тасралтгүй F(x) функцыг f(x) ийн эх функц гэнэ.
бол тасралтгүй F(x) функцыг f(x) ийн эх функц гэнэ.
Жишээ
(-∞,+∞) мужид 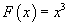 функц нь
функц нь 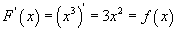 учраас
учраас 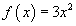 ын эх функц болно. Мөн түүнчлэн x3+13 ийн уламжлал нь 3x2 тул x3+13 нь
ын эх функц болно. Мөн түүнчлэн x3+13 ийн уламжлал нь 3x2 тул x3+13 нь 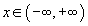 болгоны хувьд 3x2 ийн эх функц нь болно. 13 оронд дурын тогтмол авч болох нь ойлгомжтой.
болгоны хувьд 3x2 ийн эх функц нь болно. 13 оронд дурын тогтмол авч болох нь ойлгомжтой.
Математикийн хичээлийн бүх сэдвийг хамарсан ерөнхий курсын хичээлүүд. Та математикийн хичээлээ давтах, бодлого бодох, шалгалтанд бэлтгэхийн тулд ерөнхий ухагдхуун, үндсэн зарчмуудын талаар тодорхой хэмжээний мэдлэгтэй байх хэрэгтэй. Манай сайтын энэ хэсэгт математикийн хичээлтэй холбогдолтой онолын материалуудыг нийтлэж байх тул эндээс та өөртөө хэрэгтэй мэдээллийг олон авна гэдэгт итгэж байна.
Танд амжилт хүсье.
Нээгдсэн тоо: 5105 Нийтийн
Нээгдсэн тоо: 7363 Бүртгүүлэх
Хэрвээ f(x) функцын уламжлал 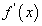 нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал /
нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал / 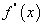 гэж тэмдэглэнэ./ гэнэ.
гэж тэмдэглэнэ./ гэнэ.
- Хэрвээ функцын график нь дурын
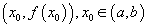 цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ.
цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ. - Хэрвээ функцын график нь дурын
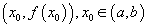 цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн дээр байрлаж байвал f(x) функцыг (a,b) интервалд хотгор гэнэ.
цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн дээр байрлаж байвал f(x) функцыг (a,b) интервалд хотгор гэнэ.
Нээгдсэн тоо: 4933 Төлбөртэй
Функцын дифференциалчлал тасалдалгүй байдлын хоорондын холбоо
Ямар нэг цэг дээр f(x) функц нь дифференциалчлагдаж байвал тэр цэгт функц тасралтгүй байна. Эсрэгээсээ энэ нь буруу байдаг. Тасралтгүй функц нь уламжлалгүй байж болно.
Мөрдлөг. Хэрвээ функц нь ямар нэгэн цэг дээр тасарч байвал энэ цэг дээр функц нь уламжлалгүй.
Жишээ
y=|x| функц нь /Зур. 3/ тасралтгүй. Гэвч x=0 цэгт функцын график нь шүргэгчгүй тул уламжлал байхгүй.
Нээгдсэн тоо: 6086 Бүртгүүлэх
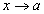 үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд
үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд 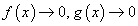 эсвэл,
эсвэл, 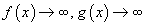 эсвэл
эсвэл 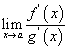 хязгаар байна.
хязгаар байна.
нөхцлүүд биелж байвал 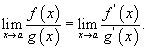 байна.
байна.
Нээгдсэн тоо: 12962 Нийтийн
Дифференцал
Функцын уламжлал 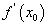 , аргументын өөрчлөлт
, аргументын өөрчлөлт 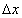 ийн үржвэрийг функцын дифференциал гэнэ.
ийн үржвэрийг функцын дифференциал гэнэ. 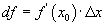
/Зур. 2 / дээр дифференциалын геометр утгыг үзүүллээ. Энд df=CD
Нээгдсэн тоо: 3984 Төлбөртэй
Уламжлал.
Ямар нэгэн f(x) функцын 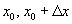 цэгүүд дээрх
цэгүүд дээрх 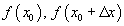 утгуудыг авч үзье.
утгуудыг авч үзье. 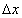 -г аргументын өөрчлөлт гэх ба аргументын бага хэмжээний өөрчлөлтийг үзүүлнэ. Цэгүүд дээрх функцын утгын ялгаварыг
-г аргументын өөрчлөлт гэх ба аргументын бага хэмжээний өөрчлөлтийг үзүүлнэ. Цэгүүд дээрх функцын утгын ялгаварыг 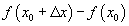 функцын өөрчлөлт гэдэг.
функцын өөрчлөлт гэдэг.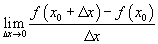 хязгаарыг x0 цэг дээрх f(x) функцын уламжлал гэнэ.
хязгаарыг x0 цэг дээрх f(x) функцын уламжлал гэнэ.
Хэрвээ энэ хязгаар нь утгатай байвал f(x) функцыг x0 цэг дээр дифференциалчлагддаг гэнэ. Функцын уламжлалыг 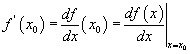 гэж тэмдэглэдэг.
гэж тэмдэглэдэг.
Нээгдсэн тоо: 8044 Бүртгүүлэх
x нь a д тэмүүлэх үед дурын ε>0 хувьд 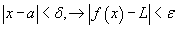 нөхцлийг хангах ε тооноос хамаарсан δ(ε) тоо олдож байвал L тоог f(x) функцын хязгаар гэнэ.
нөхцлийг хангах ε тооноос хамаарсан δ(ε) тоо олдож байвал L тоог f(x) функцын хязгаар гэнэ.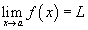 гэж тэмдэглэнэ.
гэж тэмдэглэнэ.
Энэ тодорхойлолт нь x нь a -д ойртох тутам f(x) функцын утга нь L тоонд хязгааргүй ойртоно гэдгийг илэрхийлж байна. Хязгаарын геометр утга нь дурын ε>0 хувьд x нь (α-δ, α+δ) мужид байхад функцын утга нь 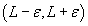 мужид орших δ тоог олж болно. Тодорхойлолт ёсоор функцын аргумент нь зөвхөн a -д ойртдог болохоос биш энэ утгыг авахгүй гэдгийг анхааралдаа авах хэрэгтэй. Энийг ямар ч функцын хязгаарыг олохдоо түүний тасралтын цэг дээр санаж байх хэрэгтэй.
мужид орших δ тоог олж болно. Тодорхойлолт ёсоор функцын аргумент нь зөвхөн a -д ойртдог болохоос биш энэ утгыг авахгүй гэдгийг анхааралдаа авах хэрэгтэй. Энийг ямар ч функцын хязгаарыг олохдоо түүний тасралтын цэг дээр санаж байх хэрэгтэй.
Нээгдсэн тоо: 4321 Бүртгүүлэх
Тоон дараалал
Натурал тоон цувааг авч үзье.
1, 2, 3, … ,n-1, n, …
Энэ цувааны тоо бүрийг тодорхой дүрмийн дагуу ямар нэгэн un тоогоор соливол шинэ тоон цуваа үүснэ.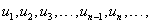 тэмдэглэгээ
тэмдэглэгээ 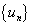
Нээгдсэн тоо: 1771 Төлбөртэй
Нэг болон хоёр үл мэдэгдэгчтэй тэнцэл биш, тэнцэл бишийн системүүдийг функцын графикаар ойролцоогоор бодож болдог. Нэг үл мэдэгдэгчтэй тэнцэл бишийг бодохдоо бүх гишүүдийг тэнцэл бишийн нэг талд гарган f ( x ) > 0 хэлбэрт оруулаад f ( x ) = 0 функцын графикийг байгуулна. Үүний дараа графикийг ашиглан функцын тэгүүдийг олно. Эдгээр нь X тэнхлэгийг хэд хэдэн хэсэгт хуваасан байх бөгөөд x-ийн аль хэсэгт функцын утга тэнцэл бишийн утгатай давхцаж байгааг тодорхойлно.
Жишээлбэл: функцын тэгүүд нь a,b /Зур. 30/ гэе. Тэгвэл графикаас f ( x ) > 0 байх хэсэг нь x<a ба x>b гэдэг нь тодорхой. Эдгээр хэсгийг тодруулсан байгаа. Энд > тэмдгийн оронд <, ≤, ≥ тэмдгүүдийн аль нь ч байж болно.
Нээгдсэн тоо: 2748 Төлбөртэй
Дурын нэг болон хоёр үл мэдэгдэгчтэй тэгшитгэл, тэгшитгэлийн системүүдийг функцын графикаар ойролцоогоор бодож болдог. Хоёр үл мэдэгдэгчтэй тэгшитгэлийн системийг бодохдоо тэгшитгэл бүрийг x ба y ээс хамаарсан функционал хамаарал гэж үзээд тэдгээрийн графикийг байгуулна. Графикуудын огтлолцлын цэгийн координат нь x ба y үл мэдэгдэгчдийн утга болно.
Жишээ 1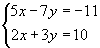 тэгшитгэлийн системийг бод.
тэгшитгэлийн системийг бод.





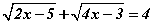 тэгшитгэл бод.
тэгшитгэл бод.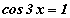 тэгшитгэл бод.
тэгшитгэл бод.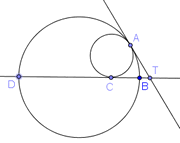 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.