Бид өмнө нь хязгаар гэж юу болох энгийн хязгааруудыг хэрхэн бодох талаар авч үзсэн. Хязгаарыг ойлгох нь хичээлд үзсэн жишээнүүд их энгийн байсан бөгөөд ийм бэлэгүүд практикт ховор тохиолдох тухай дурдсан. Тэгэхлээр энэ хичээлд хязгаарын илүү нарийн төрлүүд, тэдгээрийг бодох аргуудын талаар авч үзэцгээе.
∞/∞ хэлбэрийн тодорхойгүй төрлийн хязгаарыг бодох.
x->∞ байх үед функц нь хүртвэр, хуваардаа олон гишүүнтийг агуулсан хязгааруудыг авч үзье.
Жишээ 1.
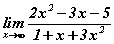 хязгаарыг тооцоол.
хязгаарыг тооцоол.





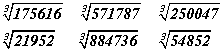
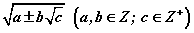
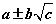 хэлбэрийн хоёр гишүүнтийн квадрат байдлаар хувиргахыг оролдох хэрэгтэй. a, b, c - том тоонууд биш байвал үүнийг амархан хийдэг. Харин a, b, c "эвгүй" өгөгдсөн бол хоёр гишүүнтийн квадратыг ялгаж чадахгүйд хүрнэ.
хэлбэрийн хоёр гишүүнтийн квадрат байдлаар хувиргахыг оролдох хэрэгтэй. a, b, c - том тоонууд биш байвал үүнийг амархан хийдэг. Харин a, b, c "эвгүй" өгөгдсөн бол хоёр гишүүнтийн квадратыг ялгаж чадахгүйд хүрнэ. болно. Эндээс тооцоог хийвэл
болно. Эндээс тооцоог хийвэл гээд л болоо. Тоо 2, 3, 4 гэх мэтээр үржигдхүүнд задарвал арга нь дажгүй. Гэхдээ нэг асуудал бий. Язгуураас гаргах тоо маань анхны тоонуудыг үржвэр хэлбэрээр задарч байвал яах вэ? Жишээ нь 152881 нь 17·17·23·23 гэж задарна. Эдгээр хуваагчийг шууд олох гээд үзээрэй. Нилээд хүндхэн байх болов уу.
гээд л болоо. Тоо 2, 3, 4 гэх мэтээр үржигдхүүнд задарвал арга нь дажгүй. Гэхдээ нэг асуудал бий. Язгуураас гаргах тоо маань анхны тоонуудыг үржвэр хэлбэрээр задарч байвал яах вэ? Жишээ нь 152881 нь 17·17·23·23 гэж задарна. Эдгээр хуваагчийг шууд олох гээд үзээрэй. Нилээд хүндхэн байх болов уу. тэгшитгэл бод.
тэгшитгэл бод. тэгшитгэл бод.
тэгшитгэл бод.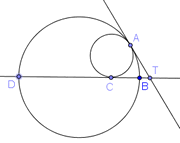 Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.
Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.